Приложение 1-2

Коэффициент η определяется по СНиП в зависимости от коэффициента заполнения: φ = (Σ A_i)/A_k = 16.38 / 81.2= 0.20∠ 0.8, и соотношения размеров поперечного сечения башни: b/h = 1.60/2= 0.80, по схеме 16 приложения 4 СНиП 2.01.07-85: η = 0.79. Здесь А_k – площадь, ограниченная контуром конструкции:

А_k = 2,0 · 40,6 = 81.2 м².

Значения коэффициента k₁ принимаются в зависимости от контура поперечного сечения и направления ветра. Для прямоугольного контура при направлении ветра, перпендикулярном грани, k₁=1.0.

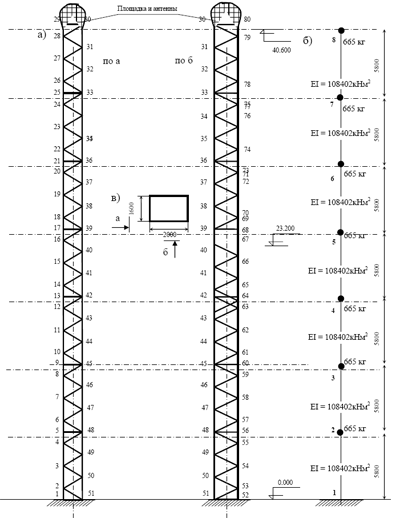
Рис. 4.5. Схема башни: а – решётка башни, б – схема башни, в – сечение ствола башни Расчетное значение средней (статической) составляющей нагрузки

S_cm = w_m= w_o c γ _f k, = 0.45·0.45·1.4· k = 0.3· k;

значения w_m в зависимости от k приведены в таблице 4.3.

Для упрощения вычисления нагрузки ферма по высоте делится на семь секций (рис. 4.5). Нагрузка на башню собирается по ее ширине в направлении, перпендикулярном потоку (2 м).

Таблица 4.3 Расчетные значения средней составляющей ветровой нагрузки

Номер узла (рис. 3.4, б)	1	2	3	4	5	6	7	8
Высота, м	0	5.8	11.6	17.4	23.2	29.0	34.8	40.6
k	0.75	0.79	1.04	1.185	1.29	1.37	1.435	1.506
wm , кПа	0.225	0.237	0.312	0.356	0.387	0.411	0.431	0.452
wm привед, кН/м	0.45	0.474	0.624	0.712	0.774	0.822	0.862	0.904

2. Определение пульсационной (динамической) составляющей ветровой нагрузки

Пульсационная составляющая ветровой нагрузки зависит от ветровых воздействий и параметров собственных колебаний башни.

Для вычисления параметров собственных колебаний башня заменяется консольным стержнем с сосредоточенными массами (рис 4.5, б). Массы сосредоточиваются в середине каждой секции (масса секции равна сумме масс всех входящих в нее стержней).

Так как размеры поперечного сечения башни постоянны по высоте, жесткость консольного стержня EI будет постоянной. Модуль упругости стали E = 210 ГПа. При подсчете моментов инерции поперечного сечения стержня учитываем только стойки башни. Тогда момент инерции сечения, образованного четырьмя стойками, относительно оси, проходящей через центр тяжести всего сечения (рис. 4.6), определится по формуле:

I_x = 4· (I_{x собств} + A· a₁ ²);

где I_{x собств} – собственный момент инерции трубчатого сечения одной стойки относительно оси, проходящей через его центр тяжести,

A - площадь поперечного сечения трубы 133 х 6, a₁ - расстояние от центра тяжести трубы до центральной оси всего сечения башни.

В результате расчетов получаем значения момента инерции и жесткости консольного стержня:

I_x = 4 · (0.0000041 + 0.002010 · 0.80²) = 0.005162 м⁴;

E_Ix = 0.005162 · 210 = 1.08402 ГНм² = 108402 кНм²;

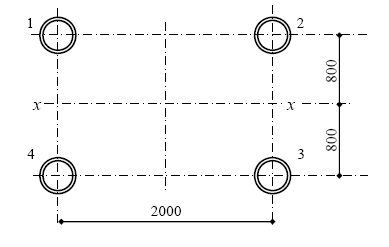
Рис. 4.6. Сечение башни

По динамической расчетной схеме определяем параметры собственных колебаний башни для первых трех форм колебаний.

Динамический расчет выполнен на ПЭВМ по программе «Динамика», составленной на кафедре Теории сооружений ДВГТУ. Полученные значения частот и периодов приведены в табл. 4.4. Формы колебаний и перемещения показаны на рис. 4.7.

Таблица 4.4 Частоты и периоды собственных колебаний башни

Форма колебаний	Круговая частота ω, с-1	Частота f, Гц (с-1);	Период Т, с
1 2 3	0.057 0.363 6.128	0.010 0.058 0.976	109.524 17.300 1.025

Для вычисления пульсационной составляющей ветровой нагрузки определяем предельное значение собственной частоты башни f_l. По табл. 8 СНиП 2.01.07-85* при δ = 0.15 (δ - логарифмический декремент колебаний, зависит от типа сооружения, принимается по СНиП 2.01.07-85*, п. 6.8) и нормативном значении ветрового напора w_o = 0.45 кПа (III ветровой район) f_l = 3.8 Гц.

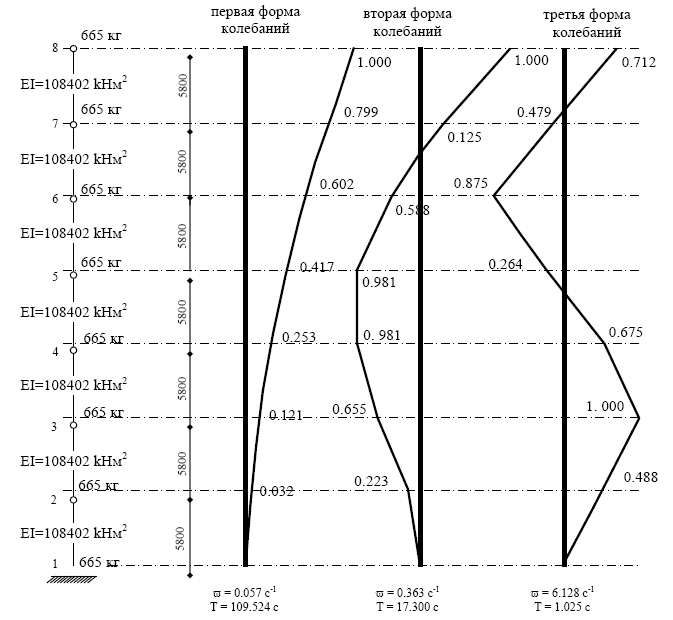
Рис. 4.7. Частоты и формы собственных колебаний башни

Так как башня имеет симметричное сечение и f₁ = 0.010 < f_l = 3.8, пульса- ционная составляющая ветровой нагрузки w_p вычисляется по формуле (здесь η = ψ, а w заменен на у, чтобы исключить путаницу в обозначениях):

wp = mξy,

где m - масса сооружения на уровне z, отнесенная к площади поверхности, к которой приложена ветровая нагрузка;

ξ - коэффициент динамичности, определяемый по СНиП 2.01.07-85* в за- висимости от параметра ξ = √( γ _fw_o)/(940f₁) и логарифмического декремента ко- лебаний δ:

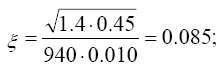
δ = 0.15 (п. 6.8 СНиП 2.01.07 – 85*);
ξ = 2.30 (п. 6.7 СНиП 2.01.07 – 85*);
y – горизонтальное перемещение сооружения на уровне z по первой форме собственных колебаний;
ψ - коэффициент, определяемый для каждого k - того участка, в пределах которого ветровая нагрузка принимается постоянной по формуле

ψ = Σy_kw_pk/Σy_k ²M_k,

где M_k - масса k-того участка,
y_k – горизонтальное перемещение k-того участка,
w_pk – равнодействующая пульсационной составляющей ветровой нагрузки для k - того участка, определяемая по формуле:
w_pk = w_mζν,
где w_m = w_okc – нормативная составляющая статической ветровой нагрузки,
ζ - коэффициент пульсаций давления ветра на уровне z, принимаемый по табл. 7 СНиП 2.01.07-85*;

В соответствии с приведенными формулами вычисляется пульсационная составляющая ветровой нагрузки, действующая на один квадратный метр вертикальной поверхности. Вычисления по высоте башни приведены в табл. 4.5.

Таблица 4.5 Пульсационная составляющая ветровой нагрузки

Номер узла	m, kH	m /Sповерхн, кПа	ξ	ψy	wp, кПа
2	6.65	0.574	2.3	0.046	0.061
3	6.65	0.574	2.3	0.173	0.228
4	6.65	0.574	2.3	0.362	0.478
5	6.65	0.574	2.3	0.597	0.788
6	6.65	0.574	2.3	0.861	1.137
7	6.65	0.574	2.3	1.142	1.508
8	6.65	0.574	2.3	1.429	1.887

3. Определение суммарной ветровой нагрузки на башню

С учетом вычисленных значений w_m и w_p, суммарная ветровая нагрузка равна:

w = w_m + w_p.

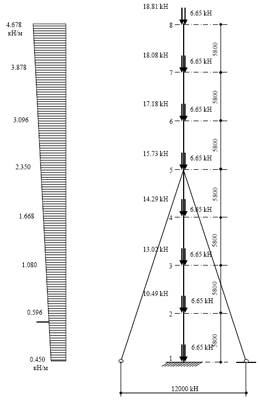
Значения суммарной ветровой нагрузки на башню для каждой секции с учетом направления ветра перпендикулярно боковой грани башни приведены в табл. 4.6, расчетная схема башни - на рис. 4.8.

Таблица 4.6 Суммарная ветровая нагрузка

Номер узла	wm, кПа	wp, кПа	w, кПа	wпривед, кН/м
1	0.225	0	0.225	0.450
2	0.237	0.061	0.298	0.596
3	0.312	0.228	0.540	1.080
4	0.356	0.478	0.834	1.668
5	0.387	0.788	1.175	2.350
6	0.411	1.137	1.548	3.096
7	0.431	1.508	1.939	3.878
8	0.452	1.887	2.339	4.678

Рис. 4.8. Расчетная схема башни