Приложение 1-2

2.10. Примеры получения частот и форм колебаний для стержней с сосредоточенными массами

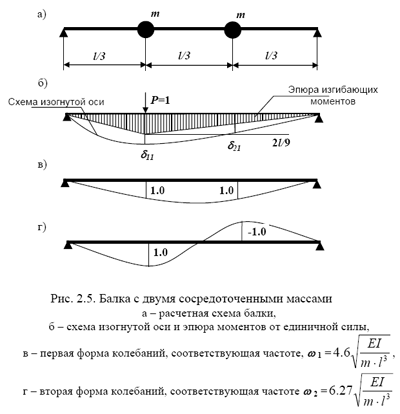
П р и м е р 2.3. Определить частоты и формы колебаний свободно опертой балки с двумя одинаковыми сосредоточенными массами, находя- щимися в третях пролета (рис. 2.5). Жесткость балки постоянна.

Р е ш е н и е. Найдем перемещения, входящие в (2.36).

Интегрирование проведено методом Симпсона⁸.

Система уравнений

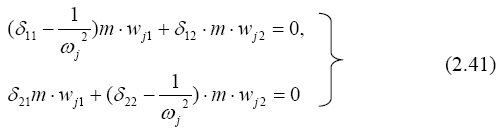
однородна, и имеет ненулевое решение, когда определитель системы равен нулю

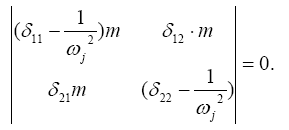
Раскроем определитель, предварительно вынесем общий множитель его элементов

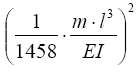
и так как он не равен нулю, то

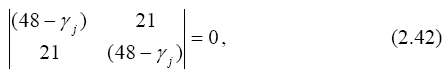
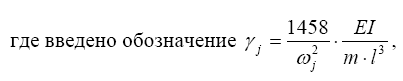
тогда определитель будет равен

(48- γ _j)· (48- γ _j) – 21² = γ _j ² - 96 γ _j +1863 = 0, (2.43)

а его корни определятся по известным формулам решения квадратного трехчлена:

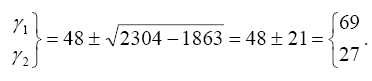
Определим частоты, исходя из того, что

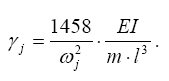
Первая (низшая) частота

Вторая частота

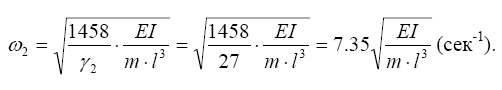
Каждой частоте соответствует своя форма. Чтобы упростить вычисления, умножим каждое из уравнений на

В результате получим для каждой частоты систему двух уравнений с двумя неизвестными

При γ ₁= 69

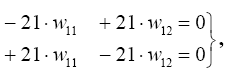
так как определитель системы равен нулю, то она имеет бесконечное мно- жество решений, поэтому зададимся значением одной из координат, на- пример, w₁₁=1.0. Тогда вторая координата определится из любого уравне- ния системы w₁₂=1.0.

Подобным образом получим вторую форму при γ ₂= 27:

Теперь зададимся значением одной из координат, например, w₂₁ = =1.0. Тогда вторая координата определится из любого уравнения системы w₂₂ = - 1.0.

Графически формы колебаний представлены на рис. 2.5.

П р и м е р 2.4 (для самостоятельного решения). Определить частоты и формы колебаний консольного стержня с двумя массами, одна из них (посредине стержня) в два раза больше другой (на конце его). Жесткость стержня постоянная.

2.11. Приведение рамных сооружений к точечным консольного типа

Для приближенной замены рамного сооружения консолью необхо- димо решить две проблемы.

• определить методику нахождения величины массы пространст- венной или плоской рамы и места ее расположения по высоте (вдоль кон- соли),
• найти жесткость консольного стержня исходя из конструктивной схемы сооружения.

Эти проблемы часто решаются интуитивно, с учетом опыта работы с динамическими схемами, но могут быть даны и некоторые рекомендации их решения путем логических рассуждений

Если, например, имеется многоэтажное здание с довольно массивными перекрытиями и оборудованием на нем, то можно достаточно обоснованно утверждать, что вся масса здания сосредоточена в уровне перекрытий и покрытия. Наибольший вклад в величину массы внесут масса самого перекрытия и оборудования, которое находится на нем. Масса ограждений мала по сравнению с массой перекрытия и она может быть отнесена к ближайшему из них по принципу равной ответственности, подобно тому, как распределяется нагрузка между несущими элементами при ее сборе⁹.

Более сложной является вторая проблема. Здесь нужно иметь ввиду то, что динамические характеристики зависят от перемещений (для точечных сооружений от горизонтальных перемещений). Чтобы динамические характеристики (частоты и формы), полученные из расчета консольного стержня были близки к характеристикам рамного сооружения, необходимо чтобы горизонтальные перемещения консоли и сооружения в уровне перекрытий были одинаковы. Из этого условия можно получить жесткости частей консольного стержня.

Имеются предложения - жесткость консоли назначать равной сумме жесткостей стоек. Однако такое решение не всегда правомерно. Специально проведенные исследования показали, что величина жесткости консоли зависит не только от жесткостей стоек, но и ригелей и способов соединений (узлов) элементов в сооружении.

Покажем применение приведенных выше рекомендаций на примерах.

П р и м е р 2.5. Построить упрощенную расчетную схему для получения динамических характеристик многоэтажного здания (рис. 1.6). Шаг рам 6 м. Жесткость одной колонны на первом и втором этажах - 1200 кНм²; на остальных этажах - 800 кНм². Ригели к стойкам крепятся шарнирно.

Р е ш е н и е . Расчетная схема здания - консольный стержень с массами, сосредоточенными в уровне перекрытий. Для получения динамических характеристик необходимо знать жесткость заменяющего раму стержня и величины сосредоточенных масс.

Рис. 2.6. Пятиэтажное трехпролетное здание: а - схема поперечной рамы; б - упрощенная расчетная схема

Жесткость на изгиб консольного стержня должна приниматься из условия, чтобы горизонтальные перемещения стержня и рамы в уровне пере- крытий были одинаковы. Часто для этого достаточно просто сложить жесткости стоек в пределах этажа. Следовательно, жесткость стержня на первых двух этажах равна

EI = 4·1200 = 4800 кНм²,

на верхних этажах

EI = 4·800 = 3200 кНм².

Сосредоточенные в уровне перекрытий массы подсчитаем по задан- ным удельным массам перекрытий и стеновых ограждений (см. рис. 2.6) и грузовым площадям при шаге рам - 6 м, трех пролетах рамы длиной - 3.6 м, высоте этажа - 3 м:

m₁ = 200·3·6·2 + 400·3.6·6· 3 = 33120 кг,
m₂ = 200·1.5·6·2 + 400·3.6·6·3 = 29520 кг.

П р и м е р 2.6. Определить жесткость консоли в упрощенной расчетной схеме в одноэтажной раме при шарнирном и жестком креплении ригеля к стойкам из условия равенства горизонтальных перемещений ри- геля (рис. 2.7).

Р е ш е н и е. Перемещение по горизонтали в уровне ригеля при шарнирном его креплении к стойкам от сосредоточенной силы ригеля - Р (на каждую стойку передается сила пропорциональная ее жесткости):

то есть, жесткость консоли должна быть равна сумме жесткостей стоек:

EI_k = EI_c1 + EI_c2 .

При жестком креплении бесконечно жесткого ригеля верхние концы стоек не поворачиваются и перемещения уменьшаются в четыре раза:

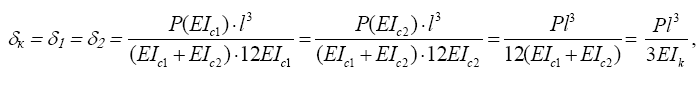
то есть жесткость консоли должна быть равна учетверенной сумме жесткостей стоек:

EI_k = 4(EI_c1 + EI_c2).

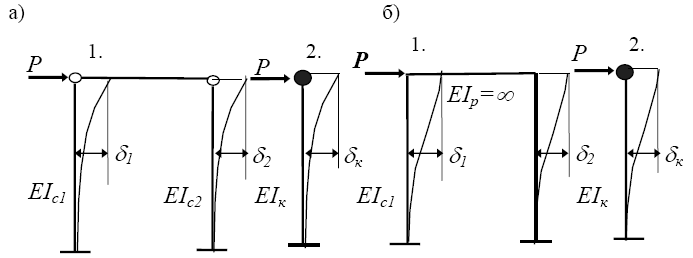
Рис. 2.7. Схемы рам с шарнирным (а) и жестким (б) креплением ригеля к стойкам: 1 – рама; 2 - заменяющая консоль

Существуют, однако, попытки совместного решения проблем внешних сил и внутренних усилий - динамический подход. Но эта сложная в математическом отношении и реализации задача решается очень редко. Примером могут служить решения, полученные одним из авторов учебника для арочных плотин и гидробиотехнических сооружений ^10,11.;