Приложение 1-2
Скачать:
Таблица 3.3 Максимальные относительные (в долях от g = 9.81 м/с2) удельные сейсмические нагрузки
![]()
приписываемые наиболее сильным землетрясениям в районах с заданной интенсивностью (балл.), возможные для площадки с грунтами второй категории 5
П р и м е р 3.1. Определить максимальную нагрузку, возможную один раз в 50 лет на объект, имеющий массу m = 120 кг, с периодом собственных колебаний Т = 0.6 с., на плотных пылеватых и маловлажных песчаных грунтах в районе с возможной сейсмичностью 7 баллов.
Р е ш е н и е. Грунты по сейсмическим свойствам относятся ко второй
категории (табл. 3.2), для которых удельная нагрузка, возможная один раз в 50
лет, равна при 7-балльном землетрясении ![]() = 0.025 (табл. 3.3). По графику на
рис. 3.6 найдем величину спектрального (динамического) коэффициента:
= 0.025 (табл. 3.3). По графику на
рис. 3.6 найдем величину спектрального (динамического) коэффициента:
β = 1/Т = 1/0.6 = 1.67.
По формуле (3.7) найдем нагрузку:
![]()
П р и м е р 3.2. (для самостоятельного решения). Определить максимальную нагрузку, возможную один раз в 20 лет на объект массой 60 тонн, находящийся на мелких водонасыщенных песках. Частота собственных колебаний четыре колебания в секунду. Объект расположен в г. Магадане.
В приведенных примерах принято среднее значение логарифмического декремента затухания, равное δ = 0.18. При меньшем или большем значении δ спектральный коэффициент β должен быть увеличен или уменьшен с помощью множителя, формулы для вычисления которого приведены в табл. 3.4.
Таблица 3.4 Формула вычисления множителя для изменения спектрального коэффициента β в зависимости от логарифмического декремента затухания δ 6
| при δ | Множитель изменения β | при δ | Множитель изменения β | при δ | Множитель изменения β |
|---|---|---|---|---|---|
| до 0.1 | 1.5 | от 0.1 до 0.2 | 1.5 - 6·(δ - 0.1) | от 0.2 | 0.9-1.3·(δ - 0.2) |
3.2. Передача сейсмического возбуждения зданию
Механизм передачи сейсмического возбуждения зданию можно представить в следующем виде. Часто участок поверхности, на котором возводится здание, относительно мал по сравнению с размерами охватываемой землетрясением поверхности земли и длиной волн распространяемых по поверхности7, поэтому введем допущение о том, что здание находится в точке на жесткой платформе. Вращением такой малой площадки будем пренебрегать и будем считать, что площадка поверхности земли, на которой находится сооружение, совершает лишь поступательные движения.
Характер поступательных движений зависит от положения площадки относительно очага землетрясения (гипоцентра) или относительно эпицентра - точки на поверхности земли над очагом.
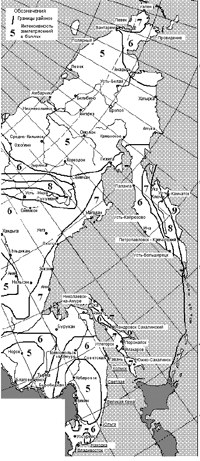
Рис. 3.7. Карта районирования территории Дальнего Востока РФ по интенсивности землетрясений
Если эта площадка находится в эпицентре, то продольные (вертикальные) волны достигают поверхности земли быстрее и сооружение начинает двигаться вертикально. Затем приходят и поперечные волны, которые вынуждают сооружение двигаться и горизонтально.
Если площадка находится вдали от эпицентра, то и продольные (вдоль луча, соединяющего гипоцентр с площадкой) и поперечные волны (поперек этого луча) вызовут и вертикальные, и горизонтальные движения (рис. 3.8).
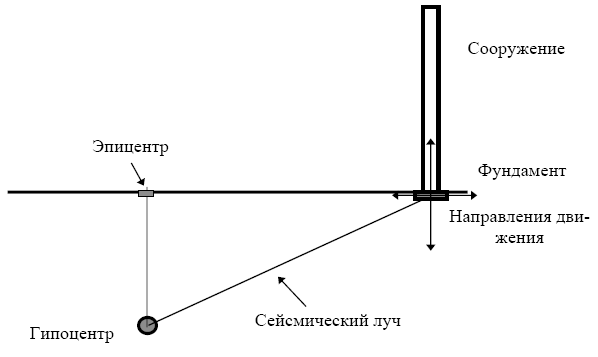
Рис. 3.8. Схема передачи сейсмического возбуждения
Как показала практика и специально поставленные эксперименты, основную опасность при землетрясениях представляют горизонтальные смещения. Вертикальную составляющую необходимо учитывать при проектировании:
- горизонтальных и наклонных консольных конструкций;
- пролетных строений мостов;
- рам, арок и ферм в конструкциях, имеющих горизонтальный пролет 24 метра и более;
- сооружений, имеющих возможность опрокинуться или сдвинуться при действии вертикальных сил;
- каменных конструкций (направление вертикальных движений принимается невыгодным для сохранения тех или иных эксплуатационных качеств сооружений).
3.3. Уравнения сейсмического движения сооружения, точечного в плане
В связи с тем, что точечное в плане сооружение находится на жесткой платформе, а сейсмическое воздействие передается через фундамент, являющийся точкой на поверхности земли, то на произвольную точку консольного сооружения, находящегося в инерционной среде с возбуждением, передаваемым через фундамент, будет действовать нагрузка, определяемая по формуле Лаппо - Морисона через параметры движения8:
- ускорение движения фундамента - ÿ0
- ускорение движения сооружения относительно фундамента - ÿ ;
- скорости движения сооружения относительно фундамента - ý
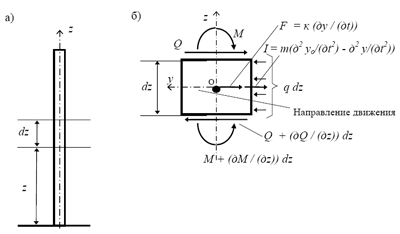
Рис. 3.9. Массивный консольный стержень (а), моделирующий точеч- ное в плане сооружение при горизонтальном движении, и его элемент (б)
Будем рассчитывать сооружение по упрощенной расчетной схеме (см. главу 1) и представим точечное сооружение как консольный стержень с распределенной массой 9.
В дифференциальной постановке уравнение движения, представляющее собой условие равновесия малого элемента под действием нагрузки в инерци- онной среде будет иметь вид10:
или после переноса в левую часть неизвестных перемещений сооружения относительно фундамента и соответствующих производных будем иметь уравнение
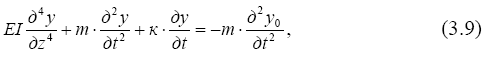
совпадающее с уравнением вынужденных колебаний стержня11 при нагрузке q(t) = −m· ÿ0.
Решение уравнения (3.9) будем искать в виде ряда
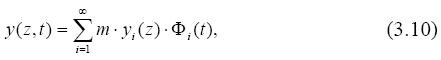
предварительно разложим нагрузку по формам колебаний
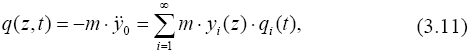
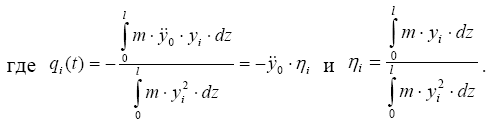
После подстановки одного из членов ряда (3.10) и (3.11) в (3.9) и деления на произведение m· yi · Φi получим равенство, каждый элемент которого не зависит от координаты и от времени, то есть, равен постоянной величине - ω i.
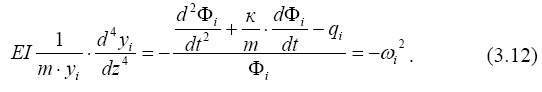
Приравняв каждую часть уравнения (3.12) постоянной величине, получим систему из двух уравнений (3.13):
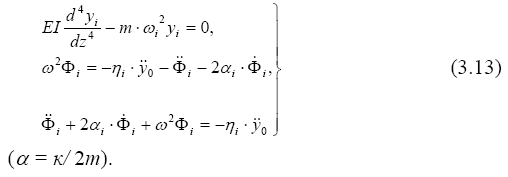
Первое из них представляет собой однородное уравнение. Ненулевым решением его являются формы колебаний соответствующие частоте ( ω i2), при которой возможно это ненулевое решение. Второе уравнение в системе упавнений (3.13), которое называют временным, по виду и решению точно совпадает с уравнением (3.2), если в нем заменить
![]()
Такое совпадение говорит о том, что записи землетрясений маятником с коэффициентом затухания, равным коэффициенту затухания сооружения, и с частотой, равной по ве- личине одной из частот его собственных колебаний, дадут график изменения функции Φ i . Следовательно, по записям землетрясений при неподвижном но- сителе можно найти максимальное отклонение Φi max:
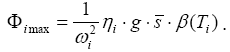
3.4. Вычисление сейсмических сил (сейсмической нагрузки). Спектральная методика
Нагрузку в инерционной среде от сейсмического воздействия определим по формуле Лаппо – Морисона
S = −m(ÿ0; + ÿ) − кý
которая с учетом разложений (3.10) и (3.11) примет вид (к = 2mα )
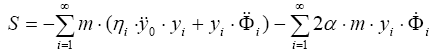
или (с учетом временного уравнения в (3.13)):
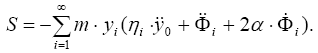
С учетом последнего равенства в (3.13):
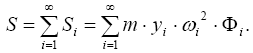
Учитывая замеченное выше совпадение уравнений движения маятника сейсмографа и временного уравнения колебания сооружения можно найти максимальное значение нагрузки соответствующее одной частоте - ω i (или перио- ду Тi = 2·π/ωi) по формуле (3.7
![]()
где т - масса сооружения, g = 9.81 м/с2 - ускорение силы тяжести, yi - координаты формы колебаний соответствующие частоте ω i ,
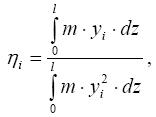
![]() - удельная сейсмическая нагрузка (табл. 3.3), зависящая от
ответственности, срока службы и допускаемых повреждений сооружений, которая определяется интенсивностью землетрясения в районе строительства (в
баллах), и расчетным периодом времени, который связан с ответственностью
сооружений и их сроком службы (см. табл. 3.5), β(Τi) или β
i - спектральный
(динамический) коэффициент, величина которого зависит от периода и степени
затухания (рис. 3.6 и табл. 3.4).
- удельная сейсмическая нагрузка (табл. 3.3), зависящая от
ответственности, срока службы и допускаемых повреждений сооружений, которая определяется интенсивностью землетрясения в районе строительства (в
баллах), и расчетным периодом времени, который связан с ответственностью
сооружений и их сроком службы (см. табл. 3.5), β(Τi) или β
i - спектральный
(динамический) коэффициент, величина которого зависит от периода и степени
затухания (рис. 3.6 и табл. 3.4).
Ориентировочные логарифмические декременты затухания (суммарные коэффициенты диссипации12) приведены в табл. 3.6.
При существующей системе наблюдений и принятой методике районирования мы можем получить только максимальные сейсмические силы, соответ- ствующие каждой форме колебаний. Такую методику вычисления сейсмических сил называют спектральной.
В спектральной методике существует проблема суммирования максимальных сил, соответствующих каждой форме колебаний, и получения расчетной сейсмической нагрузки. Здесь существует множество подходов, предлагаемых авторами на основе в той или иной степени обоснованных предложений.
3.5 . Расчетная сейсмическая нагрузка. Принципы суммирования максимальных сейсмических сил, посчитанных по спектральной методике
Ниже мы разберем три принципиально различных предложения российских специалистов о суммировании максимальных сейсмических сил.
Методика С.В. Медведева основывается на предположении, что сопротивление движению сооружения в инерционной среде мало и возможно, что максимальные силы, соответствующие разным частотам появятся одновременно.
Таблица 3.5 Расчетный период времени, определяющий относительные удельные сейсмиче- ские нагрузки для зданий и сооружений
| Класс | Допускаемые повреждения зданий и сооружений | Коэффициент К1 по СНиП Расчетный период времени |
|---|---|---|
| 1 | Сооружения, в которых остаточные деформации и локальные повреждения (осадки, трещины и т.п.) не допускаются (атомные станции, химические заводы, крупные гидротехнические и военные объекты, сооружения связи) | 1.0 (свыше 100 лет) |
| 2 | Здания и сооружения, в конструкциях которых могут быть допущены остаточные деформации, трещины, повреждения отдельных элементов, затрудняющие нормальную эксплуатацию, при обеспечении безопасности людей и сохранность оборудования (жилые, обще- ственные, производственные здания и сооружения, гидротехнические и транспортные сооружения, системы энергоснабжения, водоснабжения, пожаротушения) | 0.25 (от 100 до 50 лет) |
| 3 | Здания и сооружения, в конструкциях которых могут быть допущены значительные остаточные деформации, трещины, поврежде- ния отдельных элементов, их смещения, временно приостанавливающие нормальную эксплуатацию при обеспечении безопасности людей (одноэтажные производственные и сельскохозяйственные здания, не содержащие ценного оборудования) | 0.12 (от 50 до 20 лет) |
| 4 | Здания и сооружения, разрушение которых не связано с гибелью людей, порчей ценного оборудования и не вызывает прекращения непрерывных производственных процессов (склады, крановые и ремонтные эстакады, малые мастерские и др.), а также временные здания и сооружения | 0.00 (менее 20 лет) |
П р и м е ч а н и е: В сооружениях второго класса выделяются:
|
||
Таблица 3.6 Параметры затухания зданий и сооружений
| Характеристика конструкций и конструктивные решения зданий | Логарифмический декремент затухания |
|---|---|
| 1. Высотные сооружения небольших размеров в плане (башни, мачты, дымовые трубы, отдельно стоящие шахты лифтов и т.п.). | до 0.1 |
| 2. Здания с одним или несколькими каркасными нижними этажа- ми и вышележащими этажами с несущими стенами, диафрагмами или каркасом с заполнением, если заполнение в нижних этажах отсутствует или незначительно влияет на жесткость. | до 0.1 |
| 3.1. Каркасные здания, стеновое заполнение которых не оказывает
влияния на его деформативность при отношении высоты стоек
к поперечному размеру в направлении действия расчетной
сейсмической нагрузки, равном или более 25. 3.2. Каркасные здания, стеновое заполнение которых не оказывает влияния на его деформативность при отношении высоты стоек к поперечному размеру в направлении действия расчетной сейсмической нагрузки, равном или менее 15. |
0.1 0.2 |
| 4.1.Здания каркасные, крупноблочные, со стенами комплексной
конструкции с числом этажей более 10. 4.2. Здания каркасные, крупноблочные, со стенами комплексной конструкции с числом этажей менее 5. |
0.1 0.2 |
| 5.1. Здания крупнопанельные или со стенами из монолитного железобетона с числом этажей свыше 12. 5.2. Здания крупнопанельные или со стенами из монолитного же- лезобетона с числом этажей менее 5. |
0.1 0.2 |
| 6. Здания с несущими стенами из кирпичной или каменной кладки, выполненными вручную без добавок, повышающих сцеплени | 0.13 |
| 7. Каркасные здания, высота которых до низа балок или ферм не более 8 м с пролетом до 18 м. | 0.28 |
| 8. Сельскохозяйственные здания на сваях-колоннах, возводимые на грунтах третьей категории по сейсмостойкости. | 0.5 |
| 9. Здания и сооружения, не указанные в позициях 1-8. | 0.18 |
П р и м е ч а н и е:
|
|
С.В. Медведев предложил находить нагрузку геометрическим суммированием:

или ввиду того, что силы, соответствующие первой частоте дают наибольший вклад в расчетную сейсмическую нагрузку, то вычислять расчетную сейсмическую нагрузку с вероятностью совпадения с первой частой равной 50%, то есть:

Л.И. Корчинский, наоборот, считает, что внутреннее сопротивление движению зданий велико, и оно должно быть рассчитано на максимальную нагрузку, соответствующую только одной частоте колебаний (чаще всего первой), то есть нагрузки действуют независимо друг от друга.
А.Г. Назаров исходит из того, что основная часть сейсмической нагрузки определяется первыми одной, двумя или тремя частотами и формами колеба- ний, соответствующими низким частотам или большим периодам. Кроме того, он в своей методике использует особенность спектральной кривой (см. рис. 3.6), которая в начале - до некоторого периода колебаний То - постоянна и равна βо .
Если наибольший период (период первой формы колебаний) меньше То, то остальные периоды и того меньше, поэтому для всех частот и форм колебаний β = β о и сумма сейсмических сил в точке k равна
![]()
но так как Σηi·yik = 1
![]()
Таким образом, сейсмическая сила прикладывается статически с коэффициентом динамичности β = β о. Такие сооружения считаются жесткими.
Если наибольший период (период первой формы колебаний) больше Т1>То, а остальные периоды меньше его, то для всех частот и форм колебаний кроме первой β = β о и сумма сейсмических сил в точке k равна
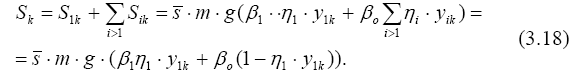
Такие сооружения считаются гибкими.
Если два наибольших периода (период первой и второй форм колебаний) больше Т1> Т2>То, а остальные периоды меньше его, то для всех частот и форм колебаний кроме первых двух β = β о, поэтому сумма сейсмических сил в точке k равна
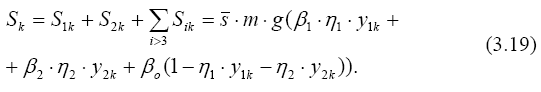
Такие сооружения считаются гибкими
Если три наибольших периода (период первой, второй и третьей форм колебаний) больше Т1 >Т2 >Т3 > То, а остальные периоды меньше его, то для всех частот и форм колебаний кроме первых трех β = β о, а сумма сейсмических сил в точке k равна
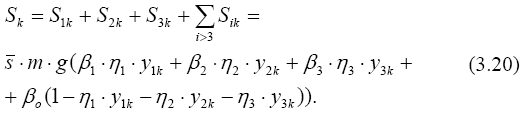
Такие сооружения считаются чрезвычайно гибкими.
К списку публикаций в разделе