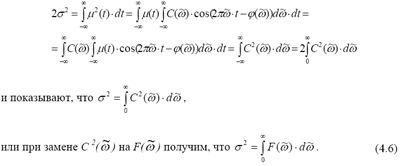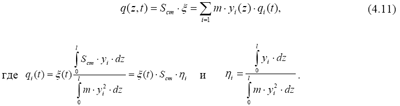Приложение 1-2
Скачать:
Глава 4. ДИНАМИЧЕСКОЕ ВОЗДЕЙСТВИЕ ВЕТРА НА СООРУЖЕНИЯ
4.1. Пульсации ветрового напора. Спектральные кривые.
В первом разделе нашего курса мы затронули вопрос об определении статической составляющей нагрузки от действия ветра1. В теории статического давления предполагается, что движение воздуха ламинарное - гладкое упорядоченное. Линии тока в таком течении параллельны между собой. Скорость движения воздуха в таком потоке изменяется по высоте из-за трения его о поверхность земли. Мы ранее обращали внимание на законы изменения скоростей по высоте в зависимости от местности, на которой находятся здания и сооружения. Давление воздушного потока пропорционально квадрату скорости и аэродинамическому коэффициенту обтекания. Этот коэффициент определяют экспериментально (например, в аэродинамических трубах).
При определенных параметрах скорости ламинарное движение воздуха становится неустойчивым. Частицы воздуха в направлении основного движения перемещаются неравномерно по изменяющимся во времени и в пространстве траекториям (внутри потока появляется беспорядочное внутреннее движение, которое называют турбулентным). Если усреднить скорость движения, то нерегулярность сглаживается, и средняя скорость вдоль потока и по высоте меняется плавно и подчиняется законам, которые мы обсуждали в упомянутом выше разделе учебника при ламинарном движении. Разность между средней и истинной скоростью называют пульсационной составляющей скорости. Для зданий и сооружений такой ветер является причиной вибрации конструкций.
В отличие от сейсмической нагрузки ветровая действует на надземную часть здания и основной вклад в нагрузку вносит скоростная составляющая. Формула Лаппо - Морисона для вычисления удельной нагрузки (приходящейся на единицу наветренной площади) имеет вид:
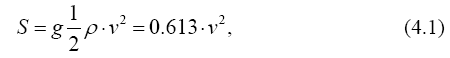
где ρ - плотность воздуха - 0.125 кг / м3, v - скорость ветра - м/с, постоянный коэффициент равен произведению известных величин 9.81·0.5· 0.125 = 0.613 Н·с2/м4.
В результате обработки данных наблюдений за ветром получены средние расчетные скорости на высоте 10 м от уровня земли на открытой местности, которые однократно превышаются в течение заданного периода времени 2 (см. табл. 4.1), и по ним любая территория может быть разделена на семь ветровых районов.
Таблица 4.1 Скорость ветра по ветровым районам на высоте 10 м на открытой местности vcp10 рассчитанная по показаниям малоинерционных анемометров 3
| Однократное превышение в период времени | номер района по карте районирования (см. Курс теории сооружений 4) | ||||||
|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | |
Год 5 лет 10 лет 20 лет 30 лет 50 лет |
17.0 20.8 22.0 23.5 24.0 25.0 |
20.0 23.8 25.8 27.0 27.4 29.2 |
23.5 27.3 29.0 31.0 31.5 32.8 |
27.0 31.3 32.8 34.2 35.0 36.5 |
30.0 34.1 36.2 38.0 38.6 40.0 |
33.1 37.7 39.5 41.2 41.8 43.2 |
36.0 40.4 44.5 45.0 45.8 48.0 |
Сама природа ветра, когда на среднюю скорость накладываются его порывы, подсказывает, что скорость можно представить в виде суммы средней скорости - vср и ее пульсационной части - vп.
Изменение средних скоростей ветра по высоте z подчиняется статистическому закону
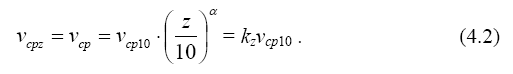
В формуле (4.2) коэффициент для открытой местности (тип А) с очень небольшими препятствиями (степь, тундра, берега и низкие острова внутренних озер) - α = 0.16;. Для местности (тип В), равномерно покрытой препятствиями высотой 10 ÷ 15 метров (жилые окраины городов, лесные массивы) - α = 0.22. Для местности (тип С) с большими препятствиями (центры больших городов) - α = 0.33 (значения kz приведены в табл. 2.8 учебника 4).
Введем в расчет коэффициент пульсации (порывистости) -μ, показывающий отношение пульсационной составляющей vn к средней скорости ветра vcp:
vnz = vcp ·μ z (4.3)
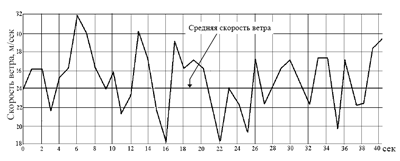
Рис. 4.1. Запись изменения скорости ветра во времени
Статистическая обработка записей распределения скорости ветра во времени (рис. 4.1) показала, что коэффициент пульсации ветра зависит главным образом от шероховатости местности. С достаточно большой надежностью можно утверждать, что максимальное значение коэффициента пульсации составляет на высоте до 10 м от поверхности земли - μ10 = 0.38, а для высот бо- лее 10 м он уменьшается по закону

где z - высота рассматриваемой точки, α = 0.16, 0.22, 0.33 в зависимости от шероховатости (типа местности - А, В, С соответственно).
С учетом уравнений (4.2), (4.3) и (4.4) можно заключить, что величина пульсационной составляющей скорости vnz мало зависит от высоты рассматриваемой точки (табл. 4.2).
Зависимость величины пульсационного коэффициента μ от времени не аналитическая, а случайная (рис. 4.1) и является отражением случайного процесса - пульсаций. Выборочную функцию случайного процесса называют случайным сигналом.
В нашем случае μ имеет среднее значение, равное нулю, оно выражает
относительное отклонение от среднего значения скорости, а среднеквадратичное отклонение его не изменяется во времени. Такой процесс называют стационарным. Стационарный процесс в практических приложениях удобно рассматривать как суперпозицию гармонических функций в непрерывном интервале частот - ![]() (или периодов -
(или периодов - ![]()
Таблица 4.2 Коэффициент увеличения скоростного напора k (вверху графы) и изменения коэффициента пульсаций ветра μ (внизу графы) по высоте
| Тип местности | Высота от поверхности земли в м | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| <5 | 10 | 20 | 40 | 60 | 100 | 200 | 300 | >480 | |
| А - незащищенная | 0.75 0.85 |
1.00 0.76 |
1.25 0.69 |
1.50 0.62 |
1.70 0.58 |
2.00 0.54 |
2.45 0.49 |
2.75 0.46 |
2.75 0.46 |
| В - с препятствиями (растительно- стью, зданиями) высотой более 10 м | 0.64 0.50 1.22 |
0.76 0.65 1.06 |
0.86 0.85 0.92 |
0.96 1.10 0.8 |
0.99 1.30 0.58 |
1.08 1.60 0.67 |
1.20 2.10 0.58 |
1.26 2.5 0.54 |
1.26 2.75 0.5 |
| С - то же высотой более 25 м | 0.40 1.78 |
0.40 1.78 |
0.55 1.50 |
0.80 1.26 |
1.00 1.14 |
1.25 1.00 |
1.80 0.84 |
2.35 0.76 |
2.75 0.68 |
| П р и м е ч а н и е. Сооружение считается расположенным в местности данного типа, если она сохраняет- ся с наветренной стороны на расстоянии 30h при высоте сооружения h < 60 м и 2 км при большей высоте. | |||||||||
С помощью известного интеграла Фурье5 уравнение этого процесса представляется суммой (в пределе интегралом) гармонических функций
![]()
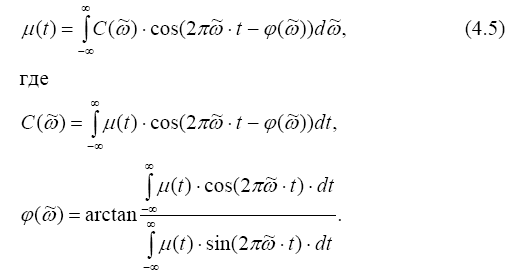
Так как среднее значение функции μ = 0, то среднеквадратичное отклонение (дисперсия) - σ·2 определится как интеграл (сумма) квадратов отклонений самой функции μ. Преобразования, произведенные с учетом соотношений (4.5), дают:
Функцию ![]() называют спектральной плотностью функции μ(t). Значение дисперсии может быть получено по уравнению
(4.6) как площади, ограниченной спектральной кривой на всем интервале реализации процесса. Из приведенных выше рассуждений следует также, что при
известной записи случайного процесса, например, в виде графика можно получить зависимость спектральной плотности от частоты (рис. 4.2), и с заданной
обеспеченностью - найти величину коэффициента пульсации.
называют спектральной плотностью функции μ(t). Значение дисперсии может быть получено по уравнению
(4.6) как площади, ограниченной спектральной кривой на всем интервале реализации процесса. Из приведенных выше рассуждений следует также, что при
известной записи случайного процесса, например, в виде графика можно получить зависимость спектральной плотности от частоты (рис. 4.2), и с заданной
обеспеченностью - найти величину коэффициента пульсации.
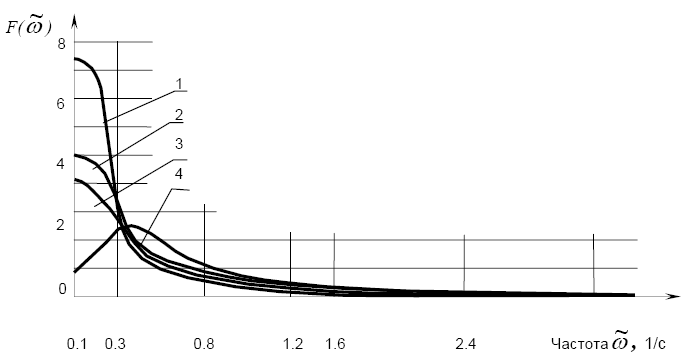
Рис. 4.2. Спектральные плотности ко- эффициента пульсации скорости вет- ра, вычисленные по четырем записям (1, 2, 3, 4) в Московской области
Таким образом, пульсационная составляющая скорости ветра характеризуется коэффициентом пульсации μ (отношение отклонения скорости ветра от среднего значения к этому значению), который может быть найден через спектральную плотность. Спектральная плотность показывает также значение коэффициента пульсации, соответствующего заданной частоте.
4.2. Уравнения движения точечного сооружения под действием ветра
Точечное в плане сооружение представляется консольным стержнем. Под действием ветровой нагрузки выше поверхности земли оно движется горизонтально, поэтому на произвольную точку консольного сооружения, находящегося в инерционной среде, будет действовать нагрузка, определяемая по формуле Лаппо - Морисона через ускорение горизонтального движения сооружения в этой точке - ÿ , скорость движения - ý и скорости перемещения частиц воздуха - v (4.1):
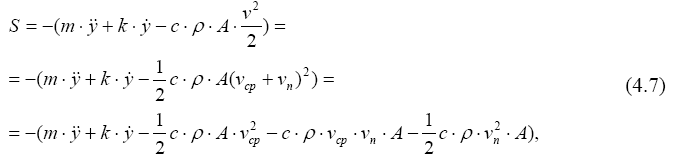
где А - площадь слоя единичной по высоте ширины наветренной поверхности, с - аэродинамический коэффициент, зависящий от формы сооружения (определяется в основном экспериментально).
Ввиду того, что расчет на статическую составляющую ветровой нагрузки ![]() может быть выполнен традиционным способом6 , по закону суперпозиции исключим эту составляющую из уравнения (4.7).
Коэффициент пульсации ветрового напора мал и поэтому нагрузку, пропорциональную квадрату пульсационной составляющей, также можно исключить, поэтому
может быть выполнен традиционным способом6 , по закону суперпозиции исключим эту составляющую из уравнения (4.7).
Коэффициент пульсации ветрового напора мал и поэтому нагрузку, пропорциональную квадрату пульсационной составляющей, также можно исключить, поэтому
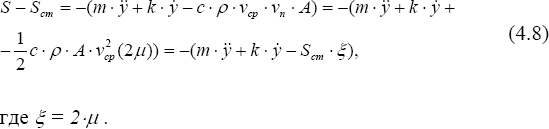
В дифференциальной постановке уравнение движения, представляющее собой условие равновесия малого элемента сооружения под действием нагрузки в инерционной среде будет иметь вид (см. главу 2):
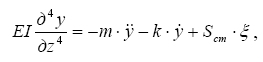
после переноса в левую часть неизвестных перемещений сооружения относительно фундамента и соответствующих производных будем иметь уравнение
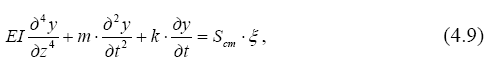
которое совпадает с уравнением вынужденных колебаний стержня при
q(t)= S cm ·ξ(t) .
Решение уравнения (4.5) будем искать в виде
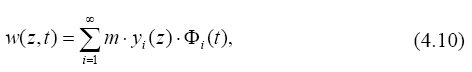
предварительно разложим нагрузку по формам колебаний
После подстановки одного из членов суммы (4.10) и (4.11) в (4.9) и деления на произведение m· w i ·Φi , получим равенство, каждая часть которого не зависит от координаты и времени, то есть равна постоянной величине:
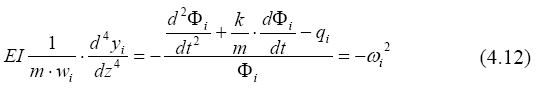
(ω i - постоянная величина – частота собственных колебаний).
Приравняв каждую часть уравнения (4.12) постоянной величине, получим два уравнения. Первое из них:
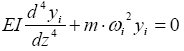
представляет собой одно- родное уравнение (ненулевым решением его являются формы колебаний соответствующие частоте ω i, при которой возможно это ненулевое решение).
Второе уравнение
![]() или
или ![]()
по виду и решению совпадает с уравнением (2.2), если в нем заменить
![]()
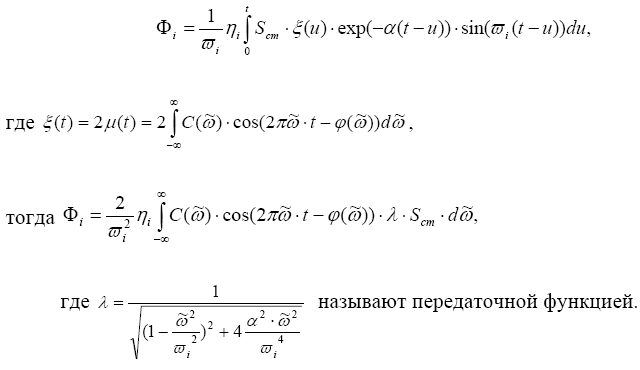
Амплитудное (максимальное) значение Фi тах можно выразить через среднее отклонение (стандарт) величины скорости от среднего значения по уравнению (3.6):
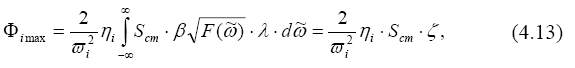
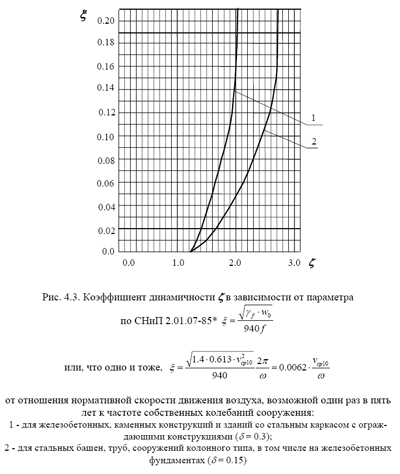
где β - число стандартов (среднеквадратичных отклонений), определяющих вероятность превышения среднего значения (при β = 3, 2.5 и 2 эта вероятность соответственно равна 0.27%, 1.23% и 4.55%); ζ - коэффициент динамичности, зависящий от логарифмического декремента затухания и отношения нормативной скорости движения воздуха, возможной один раз в пять лет (табл. 4.1) к частоте собственных колебаний сооружения (рис. 4.3).
4.3. Нагрузка от воздействия порывов ветра. Спектральная методика
Динамическую составляющую от порывов ветра определим в инерционной среде по формуле Лаппо - Морисона (4.7):
Sдин = S - Scm =-(m·ÿ+k·ý-Scm·ξ),
которое с учетом разложений (4.10) и (4.11) примет вид (к = 2mα )
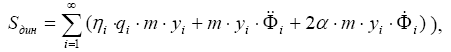
или с учетом вида временного уравнения в (4.13):
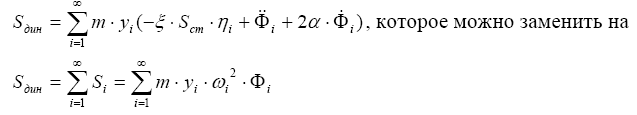
Учитывая замеченное выше совпадение уравнений движения при сейсмическом (2.2) и ветровом воздействиях можно найти максимальное значение нагрузки, соответствующее одной частоте - ω i (или периоду Тi = 2·π/ωi):
Simax =m·yi·ω2i·Φimax=m·ηi · yi · Scm·ζ (4.14)
где т - масса сооружения, yi - координаты формы колебаний, соответствующие
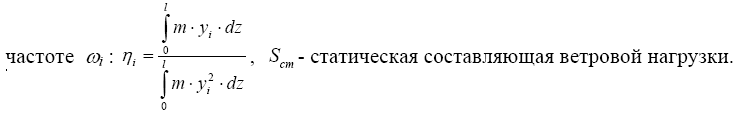
Как видно из зависимости величины спектральной плотности от частоты (рис. 4.2), спектральная плотность и, следовательно, отклонение от средней скорости значительно при малых частотах (больших периодах) и практически равно нулю при больших частотах (малых периодах). Предельное значение частот с минимальной плотностью, полученное путем обработки многочисленных записей скорости ветра, показывает, что оно зависит от средней скорости ветра, а вклад в нагрузку зависит от передаточной функции, на которую влияет степень затухания (рис. 4.4) (характеризуемая, например, логарифмическим декрементом - δ).
В расчетах на ветровую нагрузку учитываются все формы колебаний, частота которых меньше предельных значений.
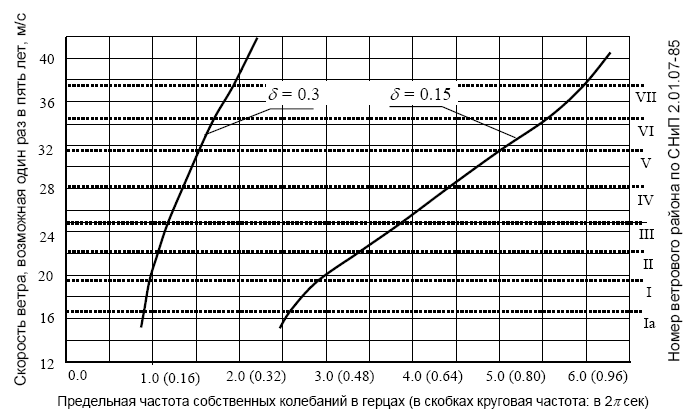
Рис. 4.4. Предельное значение собственной частоты, при котором допускается не учитывать силы инерции от порывов ветра
4.4. Методика и примеры определения ветровой нагрузки на сооружения
Методику определения ветровой нагрузки покажем на примерах высотных сооружений.
П р и м е р 4.1. Определить ветровую нагрузку на решетчатую радиотрансляционную башню в г. Уссурийске. Высота башни 40.6 м (рис. 4.5). Четыре стойки выполнены из трубы диаметром 133мм с толщиной стенки 6 мм. Решетка исполнена из труб диаметром 89мм с толщиной стенки 4.5 мм.
Р е ш е н и е . Ветровая нагрузка определяется как сумма средней (статической) и пульсационной составляющих.
1. Определение средней (статической) составляющей ветровой нагрузки
Расчетное значение средней составляющей нагрузки, распределенной по площади, вычисляется по формуле СНиП 2.01.07-85*:
Scm = wm = wo·k·c·γf
через wo – нормативное значение ветрового давления, принимаемое в зависимости от ветрового района, k – коэффициент, учитывающий изменение ветрового давления по высоте, принимается по табл. 6 СНиП 2.01.07-85*, c – аэродинамический коэффициент, зависящий от схемы сооружения, принимается по приложению 4 СНиП 2.01.07-85*, γf – коэффициент надежности по нагрузке, принимаемый для ветровой нагрузки равным 1.4.
Нормативное давление ветра для третьего района (г. Уссурийск) wo = 0.45 кПа. Коэффициент k учитывает изменение ветрового напора по высоте и зависит от типа местности. Башня находится на открытой площадке, что соответствует типу местности А.
Аэродинамический коэффициент c для решетчатой башни определяется по формуле:
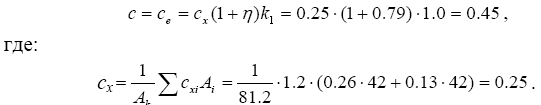
Коэффициент сxi – аэродинамический коэффициент i–го элемента конструкций, для трубчатых элементов определяется по графику к схеме 14 приложения 4, СНиП 2.01.07-85* в зависимости от числа
![]()
(d = 0.133 м – диаметр; для высоты 40.6 м - k = 1.51) следовательно, сxi = 1.2); Аi - площадь проекции i - го элемента на плоскость конструкции (на напорной грани по высоте башни стойки состоят из 42 элементов трубчатого сечения длиной 1.94 м каждый: Аi = 0,133·1.94 = 0.26 м2;на напорной грани башни имеется 42 раскоса трубчатого сечения длиной 2.23 м каждый, Аi = 0,054·2.23 = 0.13 м2).
К списку публикаций в разделе