Приложение 1-2

2.5. Разложение функции по главным формам колебаний

Ортогональность главных форм колебаний позволяет раскладывать произвольную функцию в ряд. Например, пусть дана функция (распределенная нагрузка) q(z,t). Представим её в виде разложения по формам колебаний:

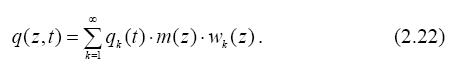
Каждый член суммы включает произведение пока неизвестного коэффициента разложения q_k(t), зависящего от времени - t, на известные функции от координат - массу и главную форму, соответствующую частоте с номером члена суммы. Вычислим коэффициенты разложения через заданную функцию. Для этого умножим обе части (2.22) на w_i и проинтегри- руем полученное выражение по всей длине стержня

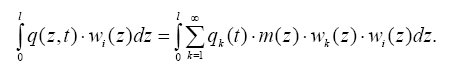
В правой части полученного выражения интеграл суммы заменим суммой интегралов и вынесем за знак интеграла коэффициенты разложения, не зависящие от координат. Тогда с учетом ортогональности форм (формула (2.21) из всей суммы останется только тот член, в котором k = i, то есть:

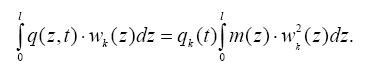
Откуда получим формулу для определения коэффициентов разложения:

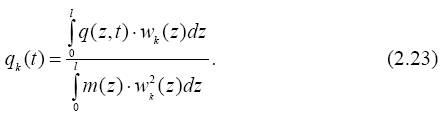
С помощью δ - функции⁴ можно записать (2.23) и для сосредоточенных функций. При этом

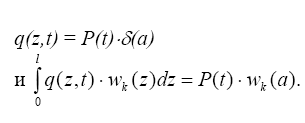
Тогда коэффициент разложения (2.23) представится в виде:

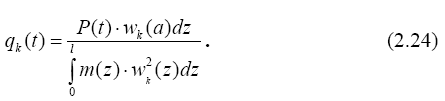
Коэффициенты разложения зависят от изменения нагрузки в пространстве. Изменение их во времени совпадает с заданным. Об этом говорит то, что при их определении интегрирование проводится по пространственным координатам.

Зависимость перемещений во времени дает решение временного уравнения, которое получается при разложении перемещений по формам колебаний и разделении переменных, проводимых по процедуре подобной предыдущим выводам (см. п. 2)

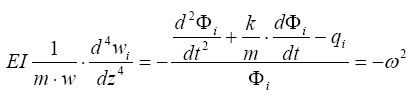
откуда:

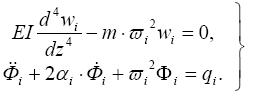
Решение временного уравнения состоит из суммы общего и частного решений:

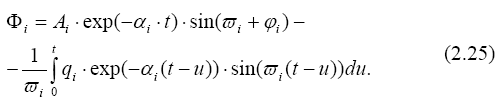
2.6. Действие вибрационной нагрузки⁵

⁵ Вибрационная (гармоническая) нагрузка (лат. vibratio - колебания) изменяется по периодическому (гармоническому) закону во времени, например, по закону синуса или косинуса: P(t) = P sin (·t). Она, в частности, вызывается механизмами, имеющими неуравновешенные массы вращающихся частей.

Тогда решение временного уравнения примет вид

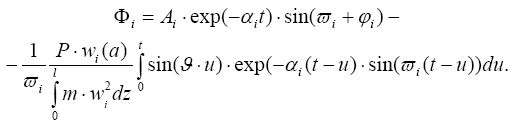
После того, как будет взят интеграл и пронято во внимание то, что общее решение при нулевых начальных условиях и на некотором протяжении затухает, это решение упростится

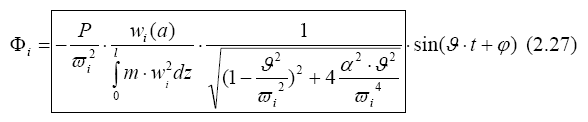
Выражение, обведенное рамкой в (2.27) не зависит от времени, и так как синус любого аргумента не может быть больше единицы, то представляет собой амплитуду колебаний. Амплитуда движения (колебания) зависит от коэффициента формы

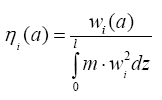
и динамического коэффициента

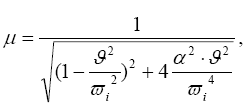
зависящего от отношения частоты возмущающей силы к собственной час- тоте и коэффициента затухания - α.

Зависимость динамического коэффициента от степени затухания и отношения частот показана в табл. 2.2 и на рис. 2.3.

Как видно из графика (рис. 2.3), при малом сопротивлении движе- нию (малом затухании) и равенстве частот возмущающей силы и собст- венных колебаний амплитуда (перемещения и усилия) движения стремится к бесконечности. Это явление называют резонансом. Для строительных конструкций резонансные явления недопустимы.

Таблица 2.2 Динамический коэффициент μ при вибрационной нагрузке в зависимости от коэффициента затухания - α и отношения частоты возмущающей силы - к частоте собственных колебаний -

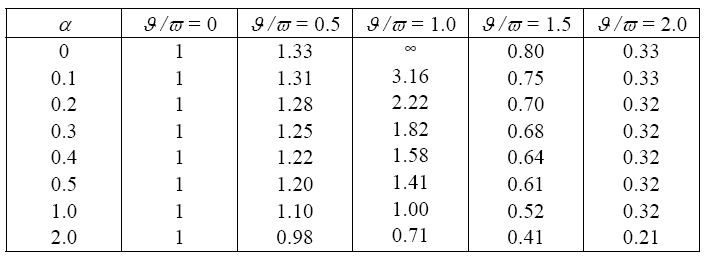
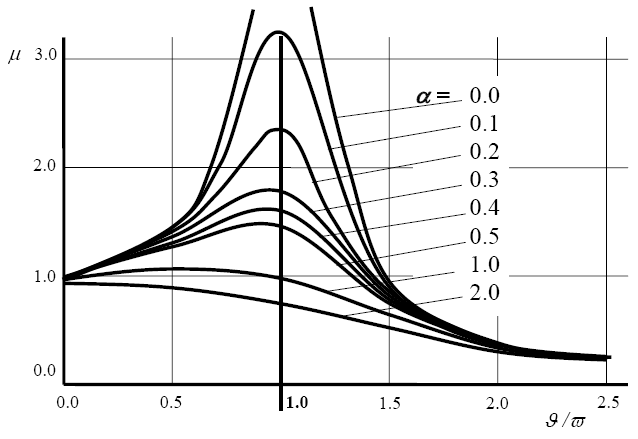
Рис.2.3. Частотные кривые при вибрационной нагрузке

2.7. Описание движения стержня с сосредоточенными массами

Часто в сооружении массы сосредоточены, например, в уровне перекрытий или покрытий зданий. Иногда приближенно заменяют распределенную массу системой сосредоточенных масс. Для таких систем имеются автоматизированные комплексы для получения частот и форм колебаний системы. Одна из таких программ для консольных стержней разработана авторами настоящего учебника⁶. Решение по этой программе приближенное. Но как показали математические эксперименты первые частоты и формы получаются практически точными при замене распределенной массы семью сосредоточенными по длине стержня.

Уравнения движения могут быть получены с помощью численных методов решения уравнений (2.4) и (2.8), но их можно вывести и отдельно, следуя процедуре, рассмотренной ранее.

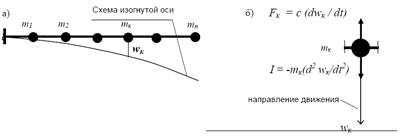
Рис. 2.4. Невесомый стержень с сосредоточенными массами (а) и силы, действующие на одну из них (б)

Рассмотрим стержень с п сосредоточенными массами (рис. 2.4). Вы- режем одну из них, например, массу к, и рассмотрим ее равновесие в инер- ционной среде. На массу действуют:

• сила сопротивления движению согласно гипотезе внутреннего трения (гипотезе Фогта) пропорциональная скорости движения и направ- лена в сторону противоположную перемещению:

F_к = с (dw_к / dt), (2.28)

где с - коэффициент пропорциональности, (dw_к / dt)- скорость движения, w_к - перемещение, t- текущее время;

• сила инерции, которая в соответствии с принципом Д’Аламбера и известному закону Ньютона пропорциональна ускорению движения

I = -m_к(d² w_к/dt²), (2.29)

где m_к – величина сосредоточенной массы, d²w_к/dt² - ускорение движения

Перемещение w_к массы m_к с учетом сил, действующих на все массы равно:

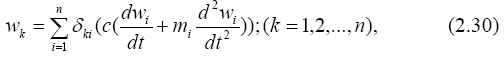
где δ_ki – перемещение точки к от сил, действующих на массу i.

Уравнение (2.30) для стержня с сосредоточенными массами эквивалентно уравнению (2.4) для стержня с распределенной массой.

2.8. Решение уравнения движения стержня с сосредоточенными массами

Уравнение (2.30) соответствует свободным колебаниям стержня (от- сутствуют внешние силы). Его решение, как и ранее, представим в виде разложения в ряд, в котором суммируются произведения функции w_jк, за- висящей только от координаты, и Φ_j (t), зависящей от времени:

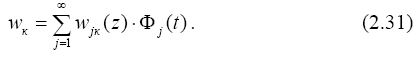
Если каждый член разложения (2.31) удовлетворяет уравнению (2.29), то полная сумма является его решением, то есть после подстановки произведения w_jк/ ·Φ_j, в (2.29) получим

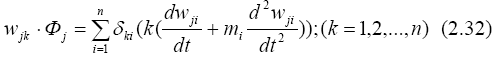
или после разделения переменных:

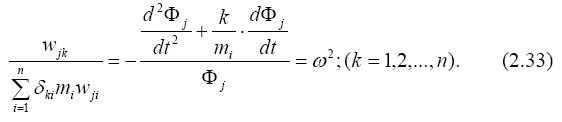
Левая часть (2.33) не зависит от времени, а правая от координаты. Равенство может сохраняться, если каждая из них - величина постоянная. Обозначим ее - ω ². Приравняв каждую часть (2.33) постоянной величине получим два уравнения:

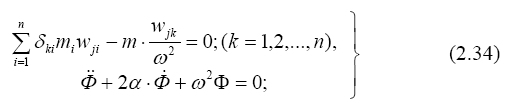
(здесь отброшен значок j, заменены производные по времени традицион- ными обозначениями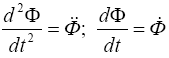

и введена постоянная 2α = k/m_i).

Второе уравнение в (2.34) называют, как и ранее, временным уравнением. Оно имеет то же решение⁷ и смысл коэффициентов (рис. 2.2):

Φ = А·ехр(-α·t) ·sin(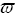·t+φ), (2.35)

2.9. Частоты и формы колебаний. Разложение нагрузки по формам колебаний

Первые уравнения (2.34) называют уравнениями форм колебаний или частотными уравнениями. Полученные уравнения однородные и имеют нулевое решение, если определитель системы не равен нулю. Это значит, что колебания отсутствуют, поэтому чтобы получить ненулевое решение, необходимо определитель системы приравнять нулю, то есть

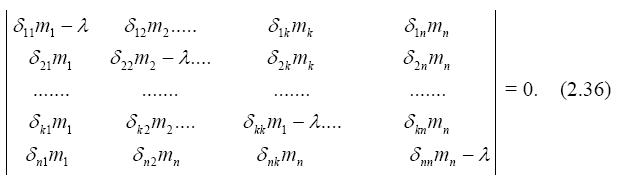
(здесь λ = 1/ω²).

В результате раскрытия определителя получим полином п – ой степени, через корни которого находятся частоты:

(здесь мы снова вернули значок j, который может принимать значения от 1 до n).

(здесь мы снова вернули значок j, который может принимать значения от 1 до n). Каждой частоте соответствует своя форма колебаний. Для того, что- бы ее получить, необходимо каждую из полученных частот подставить в систему уравнений (2.34) и решить эту систему. В результате получим перемещения всех точек сосредоточения масс системы с точностью до про- извольной постоянной величины.

Эти формы обладают свойством ортогональности, которое записывается в виде (по сравнению с условием ортогональности (2.18) только заменяется интеграл суммой):

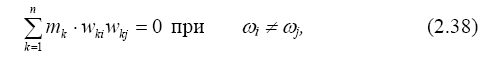
Любая сосредоточенная внешняя нагрузка может быть разложена по формам колебаний в виде

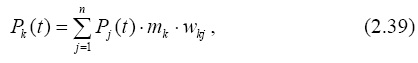
при этом коэффициенты разложения определятся по формуле

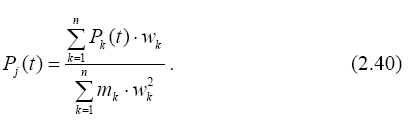
При вибрационной нагрузке в системах с сосредоточенными массами также возможен резонанс.