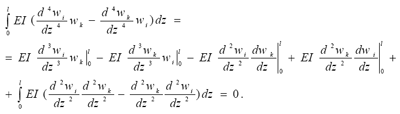Глава 2. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ СООРУЖЕНИЙ КОНСОЛЬНОГО ТИПА. ПРИВЕДЕНИЕ СООРУЖЕНИЙ К КОНСОЛЬНОМУ ТИПУ

2.1. Описание движения массивного стержня

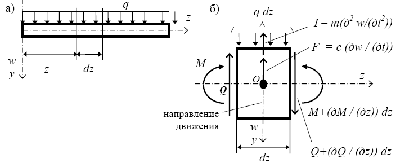
Пусть дан массивный стержень (рис. 2.1), совершающий движение под действием внешней нагрузки. Рассмотрим равновесие малого элемента этого стержня длиной dz. К нему приложены: внешняя нагрузка, сила сопротивления движению F и инерционная сила I. Сила сопротивления движению, согласно гипотезе внутреннего трения (гипотезе Фойгта) пропорциональна скорости движения и направлена в сторону, противоположную перемещению:

F = с (дw / (дt)), (2.1)

где с - коэффициент пропорциональности, дw/(дt) - скорость движе- ния, w - перемещение, t - текущее время.

В эту же сторону направлена и сила инерции, которая в соответст- вии с принципом Д’Аламбера и известным законом Ньютона пропорцио- нальна ускорению движения:

I = m(д² w/(дt²)), (2.2)

где m - масса единицы длины стержня, д²w / (дt²) - ускорение движения.

Рис. 2.1. Массивный стержень (а) и его элемент (б)

Силы, приложенные к элементу, заменяют внешнюю среду, включая и инерционную, поэтому можно рассматривать равновесие невесомого элемента в пустоте. Для плоской системы сил запишем три уравнения:

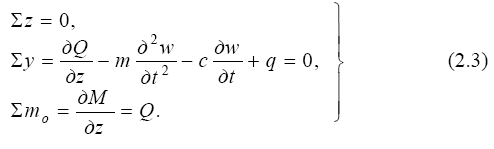
Известно геометрическое соотношение (ρ - радиус кривизны) для стержня:

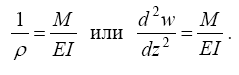
после подстановки его во второе уравнение (2.3) и несложных преобразований получим (EI = const) уравнение движения массивного стержня по- стоянного сечения:

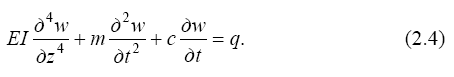
2.2. Решение уравнения движения массивного стержня

Решение полученного уравнения (2.4) будем искать в традиционном порядке. Сначала найдем решение однородного уравнения

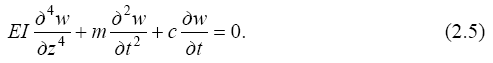
Это уравнение соответствует свободным колебаниям стержня (от- сутствуют внешние силы q = 0). Его решение представим в виде разложения в ряд, в котором суммируются произведения функции w_i (z), зависящей только от координаты, и Φ_i (t) - зависящей от времени:

Если каждый член разложения (2.6) удовлетворяет уравнению (2.5), то полная сумма является его решением.

То есть, после подстановки произведения w_i·Φ_i в (2.5) получим

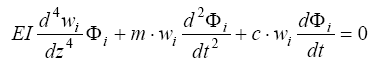
или после разделения переменных:

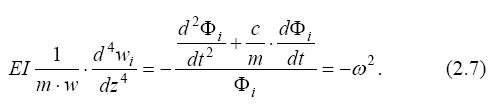
Левая часть уравнения (2.7) не зависит от времени, а правая – от координаты. Равенство может сохраняться, если каждая из них - величина постоянная. Обозначим её ω². Приравняв каждую часть (2.7) постоянной величине, получим два уравнения:

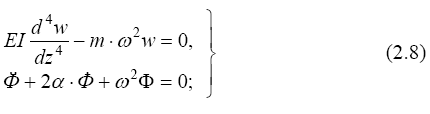
(здесь отброшен значок i, заменены производные по времени традиционными обозначениями

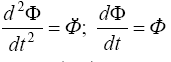
и введена постоянная 2α = с/m).

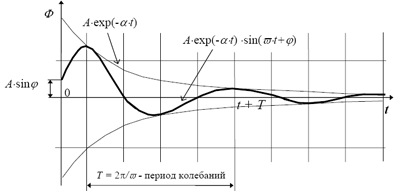
Второе уравнение в (2.8) называют временным уравнением. Оно имеет известное решение¹ (рис. 2.2):

где А и φ - постоянные интегрирования, определяемые из начальных условий движения; А·ехр(-αt) - амплитуда колебаний, затухающая со вре- менем (при t → ∞ величина А·ехр(-αt) → 0), φ - начальная фаза движения (при t = 0 величина Φ = А·sinφ), 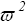= ω²-α² - круговая частота колебаний - количество колебаний в 2π секунд (количество колебаний в секунду - количество герц - равно частному от деления круговой частоты 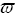на 2π - n= = 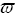/ 2π).

Рис. 2.2. График решения временного уравнения

2.3. Частоты и формы колебаний

Первое уравнение (2.8) называют уравнением форм колебаний или частотным уравнением. При постоянной по длине жесткости стержня и массе оно имеет решение²

w =A ch (sz) + B sh (sz) + C cos (sz) +D sin (sz), (2.10)

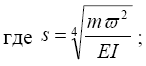
A, B, C, D - постоянные интегрирования, определяемые из граничных условий.

В постановке и решении конкретных задач по определению динами- ческих характеристик необходимо уметь формулировать начальные и граничные условия для стержней. На примерах покажем процедуру определе- ния динамических характеристик с использованием уже полученных ре- шений.

П р и м е р 2.1. Определить частоты и формы колебаний защем- ленного по двум концам стержня постоянного поперечного сечения дли- ной l.

Р е ш е н и е . Запишем граничные условия для уравнения (2.10):

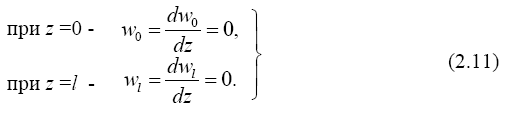
Из этих условий получим систему четырех уравнений для определе- ния четырех постоянных A, B, C, D:

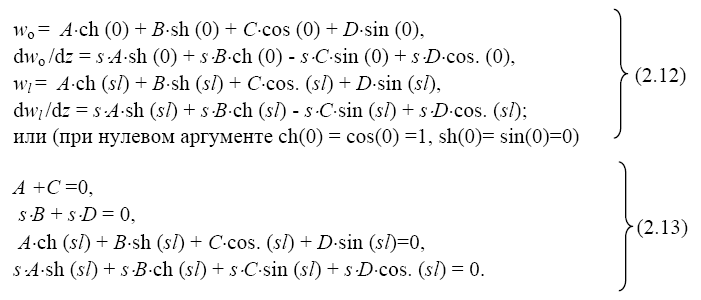
Полученные уравнения однородные и имеют нулевое решение, если определитель системы не равен нулю. Это означало бы, что колебания отсутствуют. Поэтому, чтобы получить ненулевое решение необходимо оп- ределитель системы приравнять нулю, то есть (λ = sl):

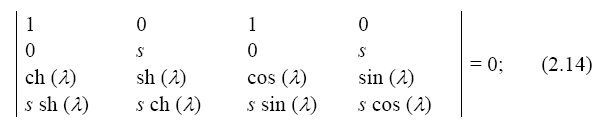
Раскроем определитель и упростим его. После раскрытия скобок и приведения подобных, получим так называемое характеристическое уравнение

- ch (λ) cos (λ) = 0, (2.15)

корни которого равны (здесь мы снова вернули значок i, который может принимать целые значения от 1 до ∞):

λ_i = s_i l = (0.5 + i)·π , (λ₁ = 4.73, λ ₂ = 7.85, λ ₃ = 11.00 и т.д.).

При таких значениях λ _i существует ненулевое решение (2.8). Учиты- вая, что

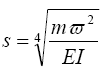
найдем по параметру λ _i частоту собственных колеба- ний:

Подставив _i или λ _i = s_i l в (2.12) найдем постоянные интегрирова- ния A_i, B_i, C_i, D_i. Но так при этом определитель системы равен нулю - она имеет бесконечное множество решений. Приходится считать одну из по- стоянных известной (например, A_i =A) и выразить все остальные через нее:

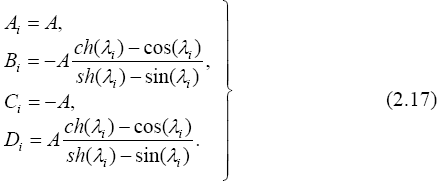
Функция прогибов, соответствующая одной из частот с учетом полу- ченных постоянных, может быть представлена в виде:

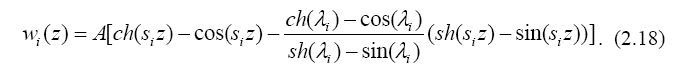
Эта функция с точностью до постоянного множителя определяет форму колебаний, соответствующую i-той частоте. Совокупность этих функций называют главными формами колебаний.

Конструкции с распределенной массой имеют бесконечный спектр частот и соответствующих им форм. В практике расчетов используются главные формы, соответствующие наиболее низким частотам. Они вносят наибольший вклад в расчетные характеристики зданий и сооружений.

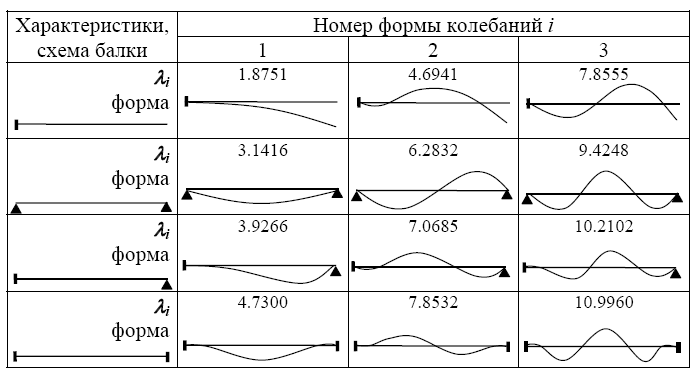
В табл. 2.1 приведены справочные данные по динамическим харак- теристикам балок с различными закреплениями.

П р и м е р 2 (для самостоятельного решения). Определить частоты и формы колебаний свободно-опертого по двум концам стержня постоянно- го поперечного сечения длиной l.

Таблица 2.1 Значения параметра λ _i для определения частот собственных попе- речных колебаний простых балок по формуле

2.4. Ортогональность главных форм колебаний

Главные формы колебаний обладают замечательным свойством - ортогональностью. Докажем это свойство. Для этого обратимся к перво- му уравнению (2.8) и запишем его для двух произвольных частот и соот- ветствующих им форм колебаний:

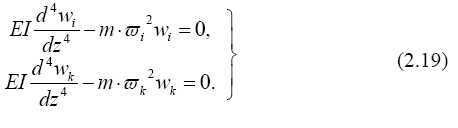
Умножив первое из них на w_k, а второе на w_i, вычтем второе из первого и проинтегрируем по длине стержня:

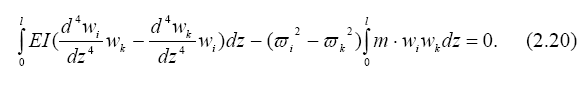
Заметим, что первый интеграл полученного уравнения (2.20) при любых граничных условиях равен нулю. Это устанавливается интегриро- ванием его по частям³:

Действительно, последний интеграл равен нулю тождественно, а первые четыре слагаемых выражают произведение усилий и перемещений по концам стержня, в котором хотя бы один из сомножителей равен нулю. В консольной балке, например, у опоры равны нулю прогиб и угол наклона (производная по z), а на конце консоли равны нулю изгибающий момент и поперечная сила (вторая и третья производные по z) .

Второй интеграл (2.20) также равен нулю в тех случаях, когда час- тоты разные по величине. И только при _i = _k интеграл может быть не равен нулю, так как равна нулю разность частот. То есть при _i ≠ _k главные формы колебаний удовлетворяют соотношению

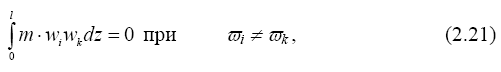
которое принято называть условием, или свойством ортогональности.