Занятие 6. ОЦЕНКА ЭКСПЛУАТАЦИОННЫХ КАЧЕСТВ СООРУЖЕНИЙ ПО СИЛОВЫМ ХАРАКТЕРИСТИКАМ ВНУТРЕННИХ СВЯЗЕЙ

Тогда для критерия наибольших линейных деформаций с учетом закона Гука (3.10) получим

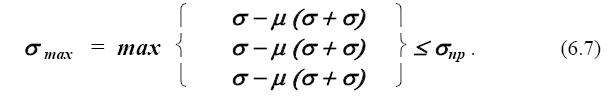
Для критерия наибольших касательных напряжений с учетом выражения (3.4)

σ _max = σ₁ − σ₃ ≤ σ_np . (6.8)

Для энергетического критерия, принимая во внимание

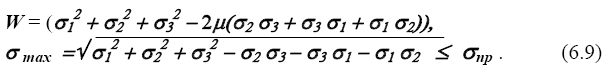
Критерии (6.3) -(6.6) принято называть предельными, так как уравнение в них ведется по предельным напряжениям.

Приведенные критерии прочности не единственные, но чаще всего используются в строительной практике. Поскольку ни один из них полностью не отражает весь сложный механизм разрушения (такого единого критерия пока нет), в случаях, когда трудно однозначно установить причину разрушения, целесообразно произвести проверку по всем критериям и за окончательное решение принять то, где разрушение наступает в первую очередь.

6.4.5. Примеры оценки прочности

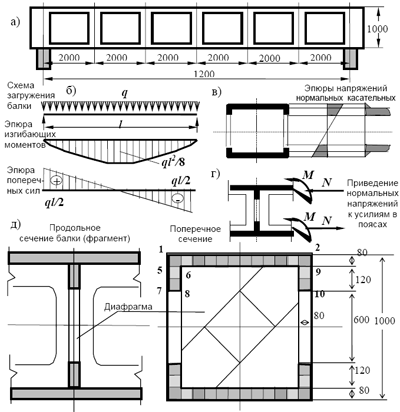
П р и м е р 6.1. Проверить прочность деревянной балки длиной 12 м со сложным поперечным сечением (рис. 6.7), загруженной постоянной равномерно распределенной нагрузкой q = 40 кН/м.

Р е ш е н и е. Определение внутренних усилий и напряжени

Балка работает на поперечный изгиб в плоскости yoz. Распределение усилий (см. п. 6.3) характеризуется по длине балки эпюрами внутренних усилий M и Q , по поперечным сечениям - эпюрами напряжений σ и τ.

Рис. 6.7. Клееная балка коробчатого поперечного сечения а - общий вид, б - расчетная схема и усилия, в - эпюры напряжений, г - усилия в поясах, д - поперечное и продольное сечения

После определения опорных реакций (V_А = V_В = 24 кН) получаем эпюры усилий, представленные на рисунке 6.7 (все необходимые для вычисления ординат расчеты читатель может легко выполнить самостоятельно, поэтому мы здесь на этих расчетах не останавливаемся).

Построение эпюр напряжений в сечениях рассмотрим подробно. Вычислим сначала все необходимые для определения σ и τ геометрические характеристики сечений (формулы см. табл.4.1). Так как сечение сложное, для вычисления момента инерции разобьем его на простые прямоугольники. Для вычисления моментов инерции каждого прямоугольника воспользуемся формулой переноса осей

I_х = I_х1 + A a² ,

где I_х1 - собственный момент инерции прямоугольника, то есть момент инерции относительно оси, проходящей через центр тяжести (оси x) прямоугольника; A - площадь прямоугольника; a - расстояние от оси x до центра тяжести прямоугольника.

I_х1295 = (1·0.08³)/12 + 0.08·1·0.46² = 0.017 м⁴,

I_х5678 = (0.08·0.12³)/12 + 0.08·0.12·0.36² = 0.0013 м⁴.

С учетом симметрии момент инерции всего сечения

I_х = 2·I _х1295 + 4·I _х5678 = 0.039 м⁴.

Статический момент определим для крайних точек (1,2), для точек, где происходит изменение ширины сечения (5,9) и для точек 8, 10 (см. Рис. 6.7). Сечение также будем считать состоящим из отдельных прямоугольников. Статический момент прямоугольника относительно оси x

S = A·a,

тогда: для точек 1 и 2 - S = 0,

для точек 5 и 9 - S = 1·0.08·0.46 = 0.0368 м³ ,
для точек 8 и 10 - S = 1·0.08·0.46 + 2·0.08·0.12·0.36 = 0.0437 м³

Наибольшие нормальные напряжения (см.п.6.3) будут возникать в поперечном сечении в середине балки в верхних и нижних волокнах, причем в этих точках положение главных площадок будет совпадать с поперечным сечением. В верхних волокнах

σ_min = σ³ = - M·h/(2·I_x) = -720·1/(2·0,039) = - 9231 кН/м²,
σ_max = σ₁ = M·h/(2·I_x) = 720·1/(2·0,039) = 9231 кН/м².

Чтобы построить эпюру σ, соединим полученные ординаты (рис. 6.7) и отбросим ту часть графика, которая оказывается в пустоте.

Касательные напряжения будут максимальными на опорах. Эпюра τ нелинейная, построим ее по точкам.

τ₁₂ = 0,
τ_{5 9 (верхний прямоугольник)} = 240·0.0368 / (0.039·1) = 226 кН/м²,
τ_{5 9 (нижний прямоугольник)}= 240·0.0368 / (0.039·0.16) = 1415 кН/м²,
τ_{8 10} = 240µ0.0437 / (0.039·0.16) = 1681 кН/м² .

Проверка прочности

С учетом действующих напряжений проверку прочности среднего сечения балки произведем на основе критерия максимальных нормальных напряжений, крайних сечений - максимальных касательных напряжений. Прочностные характеристики древесины принимаем по таблице 5.3; расчетное сопротивление при растяжении вдоль волокон R^р _пр = 10 МПа = 10000 кН/м² , при сжатии вдоль волокон R^с _пр = 14 МПа = 14000 кН/м² , при скалывании R^s _пр = 1.8 МПа = 1800 кН/м. При этих характеристиках

σ₃ = - 9231 кН/м² < R^c _np = 14000 кН/м² ,
σ₁ = 9231 кН/м2 < R^p _np = 10000 кН/м² ,
τ_max = 1681 кН/м2 < R^s _np = 1800 кН/м² .

Таким образом, условия прочности в опасных сечениях выполняются.

Умение анализировать влияние различных факторов на прочность сооружения позволяет перейти от поверочного расчета к задачам проектирования оптимальных конструкций. Чаще всего при этом приходится искать ответы на следующие вопросы.

Что сделать, чтобы при заданных условиях загружения конструкция оставалась прочной?

Какое по форме и размерам должно быть сечение?

Какой выбрать материал?

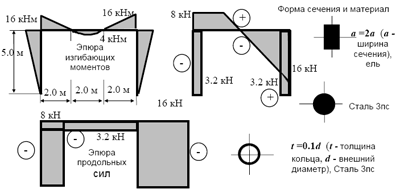
П р и м е р 6.2. Для прямого стержня по заданной эпюре моментов (рис.6.8) определить рациональное распределение материала вдоль оси.

Р е ш е н и е. Исходя из критерия оценки прочности по наибольшим нормальным напряжениям

σ = M / W ≤ R,

где σ - действующее напряжение, M - изгибающий момент, W - момент сопротивления стержня (для стержня прямоугольного сечения W= bh² /6, см. табл. 4.1), R - расчетное (предельно допустимое) напряжение. При постоянной ширине стержня прямоугольного сечения b получим его высоту

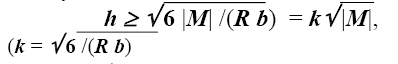
Оптимальная высота сечения, соответствующая заданной эпюре, показана на рисунке 6.8.

В некоторых случаях повышение прочности достигается неожиданными, на первый взгляд, приемами.

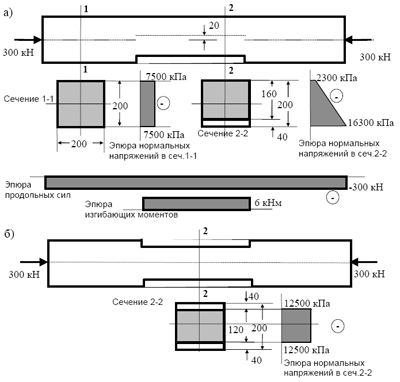
П р и м е р 6.3². Проверить прочность короткого деревянного бруса квадратного сечения 20 х 20 см, ослабленного односторонней врезкой

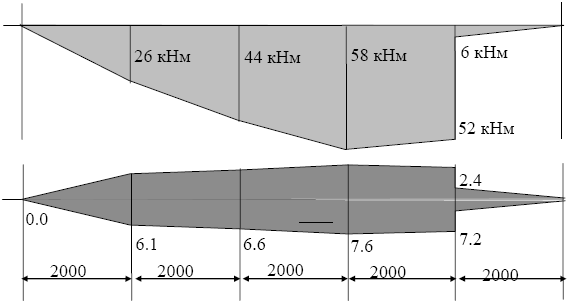
Рис. 6.8.Конструктивный образ бруса прямоугольного сечения постоянной ширины а - эпюра изгибающих моментов, б - изменение относительной высоты бруса (h/k)

Рис. 6.9. Деревянный брус с односторонней (а) и двусторонней врезкой (б)

глубиной h = 4 см. Стержень сжимается продольной силой |N| = 300 кН (рис.6.9). Расчетное сопротивление древесины сжатию Rпр = 15 МПа.

Р е ш е н и е. Напряжение в неослабленном сечении

|σ| = |N|/A = 300/(0.2· 0.2) = 7.5 МПа < R_пр = 15 МПа.

В ослабленном сечении за счет смещения его центра тяжести появляется изгибающий момент

M = 300·0.02 = 6 кНм.

Рис. 6.10. Эпюры усилий, материал и формы поперечных сечений стержней прямоугольной рамы

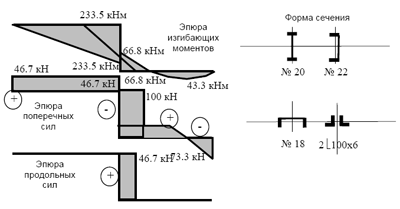
Рис. 6.11. Эпюры усилий и формы поперечных сечений стержней рамы (материал сталь 10ХСНД)

С учетом действия N и M напряжение сжатия

|σ| = |N|/A + M/W = 300/(0.2· 0.16) + 6· 6/(0.2·0.16) = 16.4 МПа > R_пр = 15 МПа,

(W = bh² /6 - момент сопротивления сечения). Такое напряжение стержень не выдержит, чтобы его снизить делается еще одна врубка сверху (рис. 6.9,б). Тогда изгибающий момент становится равным нулю, и напряжение снижается:

|σ| = |N|/A = 300/(0.2·0.12) =12.5 кН/см < R_пр = 15 МПа,

то есть условие прочности удовлетворяется.