Занятие 6. ОЦЕНКА ЭКСПЛУАТАЦИОННЫХ КАЧЕСТВ СООРУЖЕНИЙ ПО СИЛОВЫМ ХАРАКТЕРИСТИКАМ ВНУТРЕННИХ СВЯЗЕЙ

6.3. Поперечный изгиб призматического стержня

В случае поперечного изгиба исследование напряженного состояния становится более сложным. Пусть заданы величина и расположение нагрузки на стержень (рис.6.3), закрепление его по концам, размеры поперечного сечения и длина. Требуется определить положение напряженных связей.

В произвольном сечении стержня возникают нормальные и касательные напряжения (табл. 4.2)

σ _z = M_x y / I_x,

τ_zy = Q_y S_x / (b I_x)

Нормальные напряжения достигают максимальных значений в крайних волокнах поперечного сечения, в которых

σ _z = M_x h / (2 I_x),

τ_zy = 0.

Следовательно, главными площадками являются поперечное сечение стержня и продольные, перпендикулярные осям x и y, плоскости:

σ₁ = σ _z = M_x h / (2 I_x),
σ₂ = σ ₃ = 0,
τ_yx= τ_xy= τ_zx = τ_xz= τ_zy= τ_yz= 0.

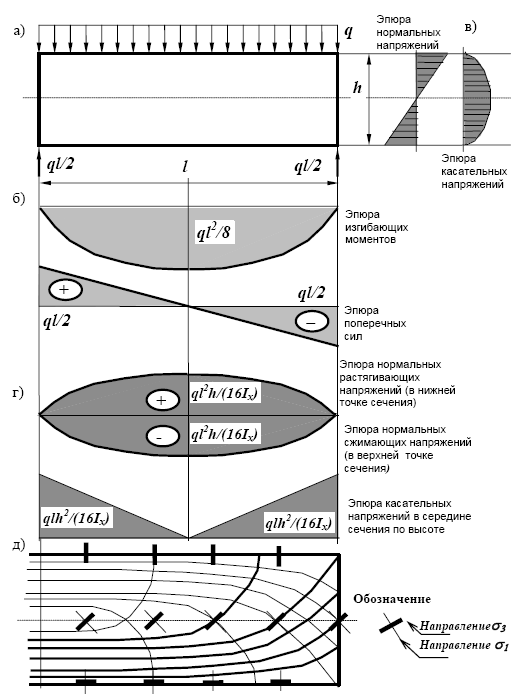
Рис. 6.3. Изгиб а - схема загружения, б - эпюры изгибающих моментов и поперечных сил, в - распределение нормальных и касательных напряжений в поперечном сечении, г - распределение нормальных и касательных напряжений вдоль стержня, д - траектории главных напряжений

Напряженное состояние крайних слоев стержня точно соответствует напряженному состоянию при центральном растяжении или сжатии. Поэтому максимальное нормальное напряжение σ_max = σ₁ расположено в поперечном сечении, а максимальные касательные напряжения - под углом α = π/4 к оси стержня и равны τ_max = σ₁ /2. По длине стержня эта точка находится в месте максимального изгибающего момента. В данном случае - посредине пролета.

На нейтральной оси сечения σ _z = 0, но максимального значения достигают касательные напряжения

τ_zy = Q_y S_x / (b I_x)

(здесь S_x - статический момент половины сечения относительно нейтральной оси). Напряженное состояние в этой точке точно соответствует напряженному состоянию при кручении. Поэтому заключаем, что касательные напряжения максимальны в поперечном сечении, а главные площадки наклонены под углом α = ± π/ 4 к оси стержня, причем главные напряжения имеют разные знаки (одно из них растягивающее, а другое - сжимающее):

τ_max = τ_zy = Q_y S_x / (b I_x),
σ₁ = − σ₃ = τ _zy .

При постоянном по длине стержня сечении максимальные касательные напряжения совпадают с максимальной поперечной силой. В данном случае поперечная сила у опор имеет максимальное значение. Таким образом, максимальные нормальные напряжения рабочего состояния возникают в месте максимального изгибающего момента в крайних волокнах поперечного сечения. Максимальные касательные напряжения - в точке с максимальной поперечной силой в середине (на нейтральной оси) поперечного сечения.

Поиск сечений, площадок, точек с максимальными напряжениями является неотъемлемой частью оценки прочности сооружения. В этом деле огромную помощь оказывают эпюры усилий, напряжений и приемы исследования этих функций на экстремум

Задача оценки прочности усложняется в связи с усложнением конструкции, нагрузок на нее и видов напряженных состояний¹.

Определив максимальные значения напряжений σ и τ, проверку условия прочности всего сооружения формально мы можем осуществить как проверку выполнения все тех же двух неравенств:

σ_max ≤ σ_np,
τ_max ≤ τ_np.

При выводе математических зависимостей между напряжениями и деформациями, описывающими внутреннее состояние стержня, принимается ряд упрощающих гипотез, в том числе исключается взаимное влияние продольных волокон друг на друга. При оценке прочности, когда речь идет уже о реальном сооружении, совсем не учитывать это влияние было бы не верно.

Решение задачи еще более усложнится, если мы будем рассматривать сложное напряженное состояние, когда одновременно придется учитывать действие разных напряжений. В этом случае всегда возникают вопросы, какой параметр выбрать для сравнения (для оценки прочности) и как учесть взаимное влияние всех параметров, определяющих напряженное состояние в точке.

Экспериментально-теоретические исследования материалов и способов оценки их прочности привели к созданию ряда критериев прочности (их часто называют теориями), основными из которых в настоящее время являются следующие.

6.4. Критерии (теории) прочности

6.4.1. Критерий наибольших нормальных напряжений

Испытания на растяжение стандартного цилиндрического образца из стали или чугуна показали, что разрушение происходит по сечению перпендикулярному к оси стержня (рис.6.4). Это приводит к выводу о том,

Рис. 6.4. Разрыв стального стержня при растяжении

что при таком способе загружения разрушение обусловлено разрывом продольных связей, воспринимающих нормальные напряжения. Такая же картина разрушения наблюдается при растяжении бетона, камня, кирпича, дерева, пластмасс.

Долгое время считалось, что разрушение нормальных связей - единственная и общая для всех материалов причина разрушения. Такая трактовка разрушения является основой критерия наибольших нормальных напряжений. Согласно этому критерию условие прочности считается выполненным, если при любом плоском или пространственном напряженном состоянии максимальные нормальные напряжение не превышают предельных.

σ_max ≤ σ_np . (6.3)

Сформулированный, как принято считать, Галилеем, критерий наибольших нормальных напряжений долгое время был бесспорным и единственным. Все возможные несоответствия между экспериментальными и расчетными напряжениями объяснялись неточностью проведения опытов или несовершенством методов расчета.

Развитие технических средств регистрации результатов экспериментов послужило толчком к более тщательному детальному изучению внутреннего поведения материала. Оказалось, поведение отдельных связей зависит еще и от того, как работают соседние связи.

6.4.2. Критерий наибольших линейных деформаций

Поиски такого показателя прочности материала, который позволил бы одновременно учесть все внутренние характеристики, привели к созданию критерия наибольших линейных деформаций, по которому предельное состояние материала наступает при достижении максимальной линейной деформацией предельной (опасной) величины. Условие прочности при этом определяется неравенством

ε_max ≤ ε _np . (6.4)

6.4.3. Критерий наибольших касательных напряжений

И в первом и во втором критериях причиной разрушения считается разрыв нормальных связей. Однако при сжатии образцов из хрупких материалов (чугуна, бетона) разрушение происходит по плоскостям, не перпендикулярным оси, а расположенным под углом, соответствующим максимальным касательным напряжениям (рис.6.5). В таких материалах слабыми являются касательные связи. Их разрушением объясняется и течение образца из упругого материала при сжатии (рис. 6.6). Важную роль касательных напряжений в оценке прочности отстаивали Ш. О. Кулон (Coulomb Chales Augustin, 1736-1806) и О. Мор (Mohr Otto, 1835-1918). Их считают создателями критерия наибольших касательных напряжений, по которому предполагается, что предельное состояние материала независимо от вида напряженного состояния (от вида деформации) наступает при достижении касательными напряжениями предельной (опасной) величины. В этом случае условие прочности имеет вид

τ_max ≤ τ _np (6.5)

Рис. 6.5. Разрушение изделий из хрупких материалов при сжатии а - цилиндр из чугуна, б - куба из бетона

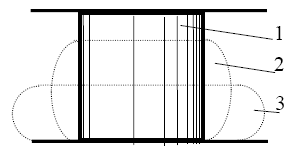
Рис. 6.6. «Течение» стального цилиндра при сжатии (1, 2, 3 - последовательное измерение формы образца)

6.4.4. Энергетический критерий

Учитывая пластическое деформирование материалов, М.П. Губер предложил в качестве фактора, определяющего наступление предельного состояния материала, принять потенциальную энергию формоизменения и считать условие прочности выполненным, если удельная потенциальная энергия формоизменения W, достигнутая в рабочем состоянии, не будет превышать предельно допустимой (опасной) W:

W ≤ W_пр . (6.6)

Критерии (6.3) - (6.6) по-разному определяют причину разрушения. Но если воспользоваться уравнениями, устанавливающими связь между параметрами напряженного состояния в точке (3.3) - (3.4), то все предельные характеристики можно выразить через усилие в одной связи. В качестве такой общей характеристики удобно принять нормальные напряжения.