Занятие 6. ОЦЕНКА ЭКСПЛУАТАЦИОННЫХ КАЧЕСТВ СООРУЖЕНИЙ ПО СИЛОВЫМ ХАРАКТЕРИСТИКАМ ВНУТРЕННИХ СВЯЗЕЙ

В соответствии с рассмотренной ранее моделью материала, свойства которого определяются характеристиками внутренних связей в рабочем и предельном состоянии, независимо от физического, геометрического или другого смысла характеристик, оценка прочности основана на проверке выполнения неравенства (1.1). Сооружение будет прочным, если максимально возможные усилия во внутренних связях не будут превышать предельно допустимых.

Неравенством (1.1) при ограниченной опорной базе можно оценить прочность либо отдельной связи (по напряжениям), либо отдельного сечения (линии) (по усилиям). Но чтобы оценить прочность всего сооружения, необходимо провести анализ распределения напряжений, усилий по всему сооружению, во всех его внутренних точках. И в каждой точке, кроме того, найти то направление, по которому связи будут максимально напряжены. Методический аппарат для этого подготовлен предыдущими рассуждениями. Ниже мы остановимся на практическом приложении этого аппарата.

6.1. Центрально загруженный стержень

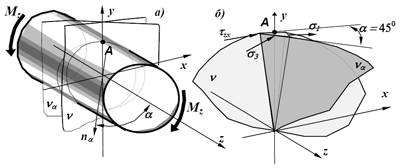
Пусть требуется оценить прочность центрально растянутого стержня (рис.6.1) при заданных размерах его поперечного сечения (h, b), длине (l) и нагрузке на одном конце (P) (второй конец закреплен).

Рис. 6.1. Растяжение а - схема загружения стержня, б - напряжения в поперечном сечении, в - напряжения в наклонном сечении

Известны характеристики прочности материала - предельно допустимые (расчетные) нормальные σ_пр = R (растягивающие) и касательные τ_пр =RS (сдвигающие) напряжения.

Растяжение стержня центрально приложенной силой мы рассматривали ранее (см. п.4.2.1) и выяснили, что продольная сила N =P (если не учитывать вес самого стержня, малый по сравнению с нагрузкой P) вдоль стержня не меняется. Поэтому мы можем рассматривать любое произвольное сечение. Нормальные напряжения во всех точках поперечного сечения одинаковы (по сечению распределены равномерно) и определяются по формуле, помещенной в таблице 4.2.

Свяжем все напряжения с осями координат стержня. В поперечном сечении, перпендикулярном оси z,

σ ₁ = N/A, τ_zx = τ_zy = 0.

В сечениях, перпендикулярных осям x и y (вдоль стержня), соответственно:

σ_х = σ_у = 0,
τ_ху = τ_zy = τ_xz = τ_zy = 0.

Так как в поперечном и продольном сечениях отсутствуют касательные напряжения, эти площадки являются главными (см. п.3.3). Значения нормальных напряжений в поперечном сечении в связи с этим являются максимальными, то есть

σ₁ = σ_z = N/A, σ₂ = σ₃ = 0.

Направления главных площадок и значения главных напряжений во всех точках стержня будут одинаковы. Любые другие площадки (не перпендикулярные осям x, y, z) не будут главными. Напряжения на них определяются по зависимостям (3.3), (3.4). Например, на площадке под углом α к оси z, для которой направляющие косинусы известны (l = cosα, m = sinα, n = 0), касательные и нормальные напряжения равны:

τ = σ₁ cosα sin α = ( σ ₁ sin 2α) / 2,
σ = σ₁ sinα

Найдем такое положение площадки (угол α), при котором касательные напряжения будут максимальными. Функция sin 2a, стоящая множителем при постоянной величине σ /2, будет иметь максимум (т. е. равна единице) при 2α = π/2 или α = π/4. Таким образом, максимальные касательные напряжения при растяжении возникают на площадках, расположенных под углом 45⁰ к оси стержня. При α = π/4

τ = τ_max = σ ₁/2 = N/(2A).

Следовательно, в растянутом стержне в каждой точке существуют две опасные плоскости с максимальными напряжениями рабочего состояния: нормальными - на плоскости, перпендикулярной оси стержня, и касательными - на площадке под углом π/4 к оси. Естественно, в рамках принятой модели материала приходим к выводу, что ввиду разных по величине предельно допустимых напряжений на растяжение и сдвиг, стержень будет прочным, если выполняются два условия:

Подобные же рассуждения можно провести и для сжатого стержня.

В стальном стержне, в котором, как показывает практика,
τ_np = 0.58σ_np ,

опасным при растяжении является сечение, перпендикулярное оси. При сжатии короткого стержня из серого чугуна, в котором

τ_np = 0.25σ_{np сжатия}

- наклонное сечение. Правда, если гибкость чугунного стержня велика, то предельное напряжение сжатия становится соизмеримым (иногда и меньшим) τ _np

Если продольная сила N и (или) площадь поперечного сечения изменяются вдоль стержня, то для оценки его прочности необходимо построить функцию N(z)/A(z) и выявить ее максимум.

Таким же образом можно проанализировать любое напряженное состояние стержня. Остановимся еще на двух.

6.2. Кручение круглого стержня

Круглый стержень длиной l и диаметром поперечного сечения D скручивается с консольной стороны моментом M _z (рис.6.2). Предельные напряжения σ_np и τ _np для материала стержня известны.

Найдем, как и в предыдущей задаче, такие точки и плоскости, в которых касательные и нормальные напряжения будут иметь наибольшие значения в рабочем состоянии. Принятые гипотезы плоских сечений дают возможность говорить о том, что во всех поперечных сечениях стержня при скручивании возникают только касательные напряжения (см. табл. 4.2)

σ_z = 0,
τ_zx = M_z y/I_p ,
τ_zy = M_z x/I_p .

Касательные напряжения будут максимальными по контуру стержня. Например, в точке A с координатами x = 0, y = D/ 2

σ_z = 0,
τ_zx = Μ_z D/(2Ι_p),
τ_zy = 0.

Рис. 6.2.Кручение а - схема загружения стержня, б - площадки главных напряжений в окрестности точки А

На площадках вдоль стержня, перпендикулярных соответственно осям x и y,

σ_x = σ_y = 0,
τ_xz = τ_zx = Μ_z D/(2Ι_p),
τ_xy = τ_yx = τ_yz = τ _{z y}= 0.

Определим по формулам (3.3), (3.4) напряжения на площадках под углом α к продольной оси (направляющие косинусы l = cosα, m = sinα, n = 0)

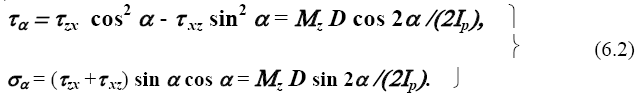
Найдем главные площадки, для этого приравняем нулю τ_α, получим cos 2α = 0 или α = ±π/4. Главные напряжения получим из соотношения (6.2) при α = π/4 и α = -π/4 (sin(2π/4) = sin(-2π/4) = 1)

σ₁ = Μ _z D/(2Ι_p),
σ₂ = − Μ _z D/(2Ι_p).

Следовательно, опасными являются точки на поверхности стержня. Для них максимальные касательные напряжения находятся на площадках, перпендикулярных оси:

τ_max = Μ z D/(2Ι_p),

а нормальные максимальные напряжения - на площадках, расположенных под углом ±π/4 (45⁰) к оси:

σ₁ = Μ_z D/(2Ι_p) (растяжение),
σ₂ = − Μ_z D/(2Ι_p) (сжатие).

Внутренние точки сечений напряжены меньше, так как касательные напряжения по мере приближения к центру тяжести сечения уменьшаются.

Проверка условий прочности (6.1) по нормальным и касательным напряжениям приводит к выводу о том, что для сталей (τ_np = 0.58σ_np) опасными будут нормальные напряжения, так как τ_max = 0.5 σ ₁. Касательные напряжения будут опасными и для серого чугуна, у которого предельно допустимые напряжения на растяжение составляют около трети сопротивления сжатию (см. табл. 5.4).