Занятие 4. ИНЖЕНЕРНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ. ВНУТРЕННИЕ УСИЛИЯ

Перед разбором примеров еще раз обратим внимание на то, что вычисления направлены на получение характеристик рабочего состояния, необходимых для проведения оценки прочности. Поэтому во всех случаях нас будут интересовать значения усилий и напряжений в опасных сечениях и в опасных точках.

П р и м е р 4.1. Короткий прямоугольный стержень сечением 20х40 см сжимается центрально приложенной силой P = 27000 кН (рис. 4.11). Определить напряжения в опасных точках.

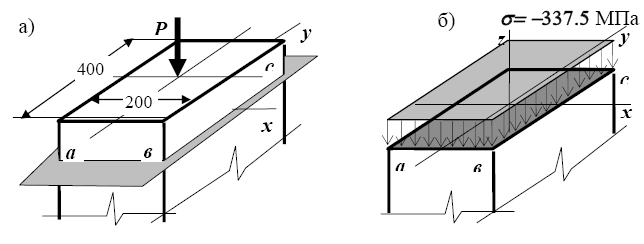
Рис. 4.11. Сжатие стержня силой, направленной по его оси а - схема загружения; б - эпюра нормальных напряжений;

Р е ш е н и е. При центральном сжатии все связи в сечениях оказываются в одинаковых условиях. Действующая постоянная по длине стержня продольная сжимающая сила

N = - P = - 27000 кН

укорачивает все связи по сечению в равной степени. Возникающие при этом силы в каждой связи - нормальные напряжения - равны

σ = -N/A = - 27000/(40·20) = -33.75 кН/см² = - 337.5 МПа.

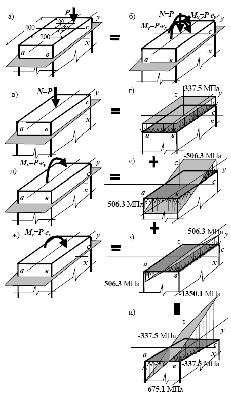
П р и м е р 4.2. Такая же сила P = 27000 кН (см. предыдущий пример) прикладывается к тому же стержню, но со смещением на e = 5 см по оси x и на e_y = 10 см по оси y (рис 4.12). Определить напряжения в опасных точках.

Р е ш е н и е. Как и в предыдущем примере, внутренние усилия по длине стержня не меняются, но в каждом сечении за счет смещения точки приложения нагрузки кроме продольной силы

N = - P = - 27000 кН

появятся изгибающие моменты

M_x = P·e_y = 27000·10 = 270000 кН·см,
M_y = P·e_x = 27000·5 = 135000 кН·см.

Значение напряжения при одновременном действии N, M_x и M_y вычисляется по формуле (см. табл.4.4)

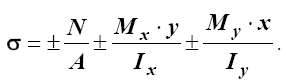
Определим необходимые для вычисления напряжений геометрические характеристики сечения (см. табл. 4.1)

A = 20·40 = 800 см²,
I_x = b·h³ /12 = 20·40 /12 = 106666.7 см⁴,
I_y = h·b³ /12 = 40·20 /12 = 26666.7 см·4.

Знак первого слагаемого в формуле определения напряжений обуславливается знаком продольной силы. В данном случае продольная сила отрицательна.

Рис. 4.12. Сжато-изогнутый стержень а - схема загружения; б - равнодействующая система сил, приведенная к оси стержня; в, д, ж - действие составляющих системы сил в отдельности; г, е, з - нормальные напряжения от действия каждой из системы сил в отдельности; и - суммарные напряжения

Поэтому наибольшее значение напряжения получится в точке, для которой второе и третье слагаемое так же будут отрицательными (под действием моментов Mx и My продольные связи будут сжиматься). Эта точка наиболее удалена от центра сечения (xmax = 10 см, ymax= 20 см). Значение напряжения в ней

σ = - 27000/800 - 270000·20/106666.7 - 135000·10 / 26666 = -135.01 кН/см² = -1350.1 МПа.

Графическое нахождение положения опасной точки показано на рисунке 4.12. Из приведенного построения следует, что такой точкой будет угловая точка с.

Обратите внимание, что по сравнению с предыдущим примером изменилась только точка приложения нагрузки. Смещение нагрузки привело к увеличению напряжения в три с лишним раза.

П р и м е р 4.3. Определить напряжения в опасных точках опасных сечений, если задан закон распределения внутренних усилий, представленный эпюрами M, Q, N, размеры стержня, форма и размеры поперечного сечения (рис. 4.13). Размеры сечения по длине стержня не меняются.

Р е ш е н и е. По таблице 4.4 определяем, что при действии на стержень M, Q, N (изгиб со сжатием) напряжения в его сечениях будут равны:

нормальные σ = N/A + M_x·y/I_x ,
касательные τ = Q_y·S_x /(I_x ·b).

Опасными мы называем такие сечения, в которых возникают максимальные усилия. Если размеры сечения по длине стержня не меняются, то положение такого сечения определяется по эпюрам усилий. По приведенным эпюрам определяем, что в данном случае имеют место три опасных сечения: 2, 4 и 3. В сечении 3 изгибающий момент максимальный и, следовательно, появятся максимальные нормальные напряжения, но касательные при этом будут равны нулю. Из всех сечений с одинаковыми значениями поперечной силы выберем такое, где действует еще и изгибающий момент, так как их совместное действие может оказаться неблагоприятным. Чтобы получить представление о работе опасных сечений, построим для них эпюры напряжений.

Вычислим необходимые для определения напряжений геометрические характеристики:

площадь сечения A = b·h = 10·20 =200 см² ,
момент инерции I_x = b·h /12 = 10·20 /12 = 6666.67 см⁴ ,
статический момент
половины сечения S_x = b· (h/2)·(h/4) = 10·10·5 = 500 см³
четверти сечения S_x = b·(h/4)·(3h/8) = 10·5·7.5 = 375 см3 .

Напряжения в сечении 3. Эпюру нормальных напряжений можно получить путем графического сложения эпюр (по табл.4.4) σ_z1 = N / A и σ_z2 = M_x·y / I_x (рис. 4.14).

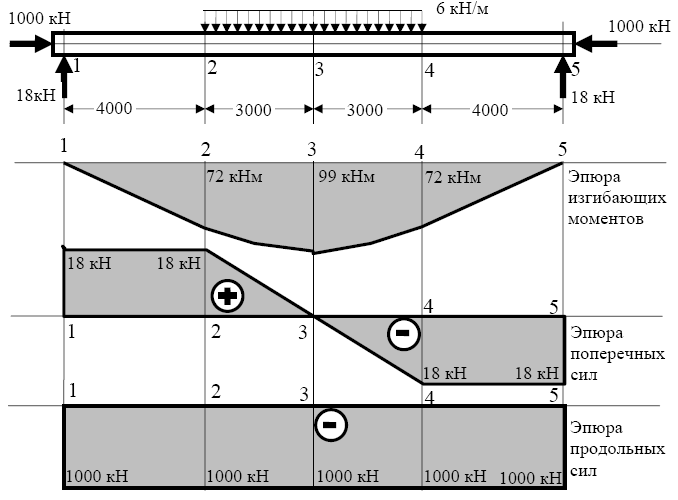
Рис. 4.13. Сжато-изогнутый стержень с эпюрами усилий

σ_z1 = N/A = - 1000/200 = - 5 кН/см² = - 50 МПа - сжимающее напряжение, равномерно распределенное по сечению;

σ_z2 = M_x·y/ I_x - зависит от y:
при y = 0 σ_z2 = 0,
при y = ±h/2 имеют наибольшие значения
σ_z2 = ±99 100·10/6666.67 = ±14.85 кН/см² = ± 148.5 МПа.

По эпюре моментов определяем знаки напряжений. Так как верхние волокна сжаты, а нижние растянуты, то соответственно напряжения σ_z2 по верхней грани сечения - σ ^в отрицательные, по нижней - σ ^н положительные

σ ^в= - 5 - 14.85 = -19.85 кН/см2 = -198.5 МПа,
σ ^н= - 5 + 14.85 = 9.85 кН/см2 = -98.5 МПа.

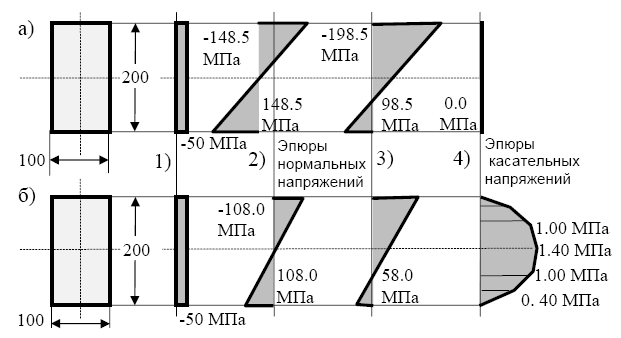
Рис. 4.14. Эпюры напряжений в сечениях 3 и 2 (см. рис. 4.13) а - сечение 3, б - сечение 2. 1, 2, 3 – соответственно напряжения от продольных сил, изгибающих моментов, суммарные, 4- касательные напряжения

Наибольшие нормальные напряжения в сечении 3 сжимают верхние волокна.

Напряжения в сечении 2 (рис 4.13в)
нормальные σ = (- 1000/200 ±7200·10/6666.67) кН/см² ,
на верхней грани σ ^в = - 5 - 10.80 = -15.80 кН/см² = -158 МПа,
на нижней σ ^н = - 5 + 10.80 = 5.80 кН/см² = - 58 МПа.

Касательные напряжения распределяются по криволинейному закону.

Эпюру напряжений построим по точкам
в середине сечения τ = 18·500/(6666.67·10) = 0.14 кН/см² = 1.4 МПа,
в четверти сечения τ = 18·375/(6666.67·10) = 0.10 кН/см² = 1.0 МПа,
в крайних точках τ = 0.

П р и м е р 4.4 (для самостоятельного решения). Проверить, как изменятся напряжения в стержне, рассмотренном в предыдущем примере, если сечение повернуть на 90^о, т. е. принять b = 20 см, h = 10 см.

Если внутренние усилия известны, то вычисление напряжений по формулам таблице 4.2 затруднений обычно не вызывает. Но для анализа работы сооружения от инженера требуется не только уметь определять значения внутренних усилий и напряжений, но и хорошо (и это, пожалуй, главное) представлять, от чего зависят их величины и характер распределения. Для приобретения навыков в решении таких вопросов предлагаем самостоятельно решить следующие примеры.