Занятие 4. ИНЖЕНЕРНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ. ВНУТРЕННИЕ УСИЛИЯ
Скачать:
Нормальные напряжения s приводятся к паре сил с моментом

который называется изгибающим моментом относительно оси x. Подставляя соотношения (4.2) в (4.3), получим
![]()
∫Ay2dA = Ix представляет собой геометрическую характеристику сечения стержня и называется моментом инерции сечения относительно оси x. С учетом этого обозначения будем иметь
Mx = E·κ·Ix . (4.4)
Знак момента определяется знаком координаты y и напряжения σ z и совпадает со знаком кривизны. Из соотношения (4.2): κ = σz / (E·y). Подставляя это выражение в (4.4), получим формулу, связывающую изгибающий момент с напряжениями в связях
Mx = σ z·I / y . (4.5)
Геометрические характеристики часто встречающихся сечений приведены в таблице 4.1, а прокатных профилей - в таблицах 4.2 и 4.3.
Таблица 4.1. Характеристики сечений
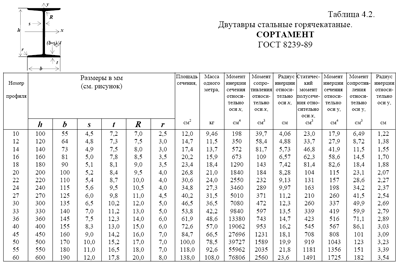
Таблица 4.2. Двутавры стальные горячекатаные. СОРТАМЕНТ ГОСТ 8239-89/p>
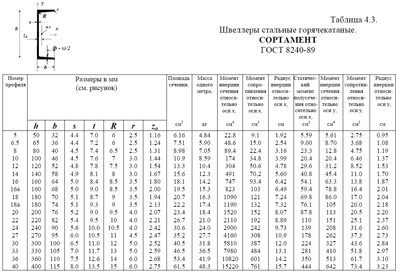
Таблица 4.3. Швеллеры стальные горячекатаные. СОРТАМЕНТ ГОСТ 8240-89
4.2.3. Сдвиг (срез)
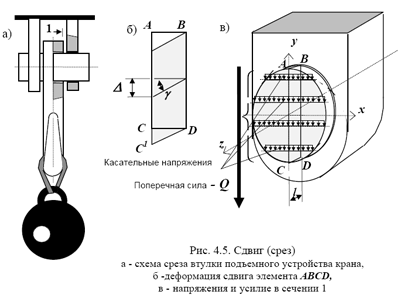
Деформацию сдвига (среза) можно наблюдать на оси грузового устройства (рис.4.5). Приложенная к крюку нагрузка будет стремиться опустить его вниз, перерезая при этом ось, поддерживающую крюк, по сечению AC, совпадающему с боковой гранью крюка. Сдвигу (срезу) волокон стержня по этому сечению будут препятствовать внутренние связи, но при этом в них появятся деформации Δ, которые принято определять через угол сдвига (рис. 4.5). В соответствии с гипотезой плоских сечений деформация сдвига для всех связей в сечении AC одинакова, а вследствие малости перемещений
γ = tg γ = Δ / l.
Рис. 4.5. Сдвиг (срез) а - схема среза втулки подъемного устройства крана, б -деформация сдвига элемента АВСD, в - напряжения и усилие в сечении 1
Все остальные деформации связей в сечении отсутствуют, то есть
εz = ε x = ε y = 0, γzx = γyx = 0 .
Если в плоскости среза разрезанные связи заменить напряжениями (рис.4.5), то в соответствии с физическими соотношениями (3.10)
σz = σ x = σ y = 0, τzy= G·γ, τzx = τxy = 0. (4.6)
Равнодействующая касательных напряжений в данном случае называется поперечной силой при сдвиге. С учетом равномерного распределения τzy по сечению ее значение будет равно
Qс д.в=∫Aτzy·dA=τzy·A. (4.7)
Знак поперечной силы определяется знаком касательных напряжений
4.2.4. Кручение круглого стержня
Деформация кручения характерна для работы валов. Примером вала является прямолинейный стержень круглого сечения, один конец его закреплен неподвижно, а к другому крепится устройство, через которое передается нагрузка, стремящаяся повернуть вал вокруг его оси (рис.4.6).
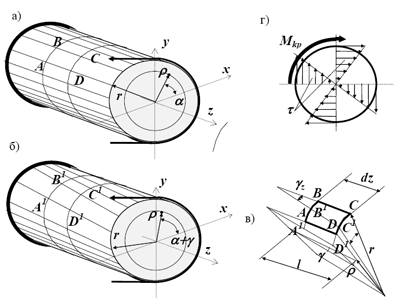
Рис. 4.6. Кручение а -общий вид стержня, б - схема скручивания, в - деформация элемента АВСD, г - касательные напряжения (τ) и усилие - крутящий момент (М кр)
При этом в стержне продольные деформации отсутствуют, то есть εx = εy = εz = 0,
а в плоскости xoy происходит сдвиг (поворот) одного сечения относительно другого (рис.4.6). Угол сдвига для каждого сечения γ и, следовательно, удлинение радиальных волокон Δ определяются общим углом закручивания стержня γ (рис.4.6). Рассматривая элементарный участок вала (рис.4.6), из простых геометрических соображений с учетом малости угла закручивания, легко установить, что tg γ = γ = Δ/l = r·d γ r /dz. Величина d γ r/dz - относительный угол закручивания - имеет размерность м-1 и обозначается обычно θ.
По соотношению (3.10) с учетом относительного угла закручивания напряжения в крайних волокнах (рис.4.6)
τr = G·θ·r,
а в произвольном сечении на расстоянии ρ от центра сечения
τρ= G·θ·ρ. (4.8)
С учетом характера распределения эти напряжения называются радиальными. Они приводятся к паре (рис. 4.6, г), называемой крутящим моментом, который определяется по формуле
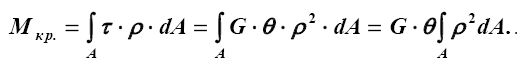
Величину ∫Aρ2dA называют полярным моментом инерции сечения и обычно обозначают через Iρ , тогда
M кр. = G·θ·Iρ (4.9)
или с учетом соотношения (4.8)

4.2.5. Поперечный изгиб
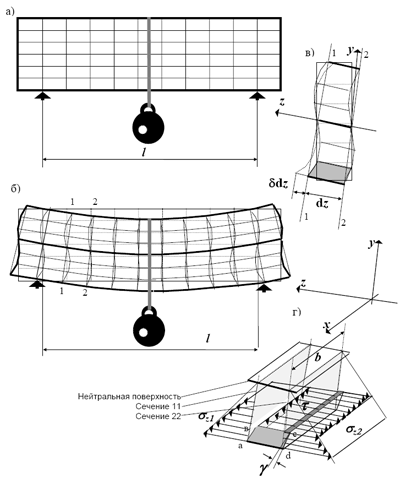
В отличие от чистого изгиба при поперечном изгибе стержня (рис.4.7) происходит не только удлинение и укорочение составляющих его волокон, но и сдвиг этих волокон относительно друг друга. Поэтому сечение разворачивается по отношению к продольной оси и искривляется (депланирует), перестает быть плоским. Гипотеза плоских сечений позволила во всех рассмотренных выше случаях получить зависимости между деформациями и напряжениями на основе простых геометрических соображений, в данном случае она оказывается неприемлемой. Дмитрий Иванович Журавский (1821-1891) предложил оригинальный выход из этого положения. Он ввел предположение, что депланация1 сечений при поперечном изгибе не оказывает влияния на нормальные напряжения в поперечных сечениях стержня, то есть, как и при чистом изгибе

а сказывается только на величине и распределении по сечению касательных напряжений τ. По Д.И. Журавскому

где b - ширина сечения в уровне действия напряжения τ, S - статический момент площади выше (ниже) этого уровня относительно центра тяжести сечения2.
2Познакомим читателя с решением Д.И. Журавского.
Вырежем из стержня элемент (рис.4.7) он принял изменяющимися так же, как и при чистом изгибе, т. е. ε = κ·y. Поэтому и распределение нормальных напряжений по высоте сечения будет таким же, как и при чистом изгибе σ = E·ε = E·κ·y. Ввиду того что при поперечном изгибе кривизна κ изменяется по длине стержня, напряжения по грани ab (сечение 2-2), которые обозначим σz2 , будут отличаться от напряжений по грани cd (сечение 1-1) - σz1. Касательные напряжения действуют по граням ab и cd - τzy и грани bc - τyz . Ввиду парности касательных напряжений τyz = τzy = τ.
Спроецируем все силы, действующие на выделенный элемент, на продольную ось стержня- z. Из условия равновесия элемента эта проекция равна нулю.
![]()
где A - площадь грани ab и cd.
Так как изгибающие моменты в сечениях 2-2 и 1-1 отличаются и, соответственно, равны M и M + dM, то по (4.11) получим
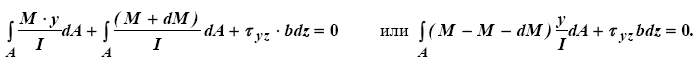
Откуда
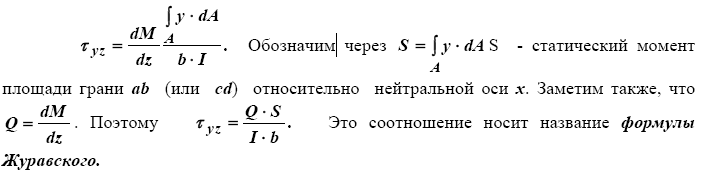
Рис. 4.7. Поперечный изгиб а - общий вид стержня, б - схема его изгибания, в - деформация элемента 1122, г - напряжения по граням параллелепипеда с основанием авсd
Равнодействующие напряжений в сечении - продольная сила N, моменты (изгибающие Mx , My и крутящий момент Mz) и поперечная сила (Qx или Qy) называются внутренними усилиями и представляют собой интегральные (суммарные) характеристики напряжений.
Для всех остальных видов деформации внутренние усилия можно получить на основе выведенных формул (4.1) - (4.12). Так как при малых перемещениях справедлив принцип суперпозиции, то все сложные деформации и соответствующие им усилия рассматриваются как сумма независимых простых деформаций или усилий. Рассматриваемые ниже виды напряженного состояния можно рассматривать как примеры использования этого принципа.
К списку публикаций в разделе