Занятие 4. ИНЖЕНЕРНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ. ВНУТРЕННИЕ УСИЛИЯ

4.1. Геометрические допущения инженерных методов

Для решения задачи оценки прочности (подробно мы будем говорить об этом в шестой главе) достаточно знать либо напряжения в связях, либо их деформации. Однако как видно из выражений (3.8), (3.10), (3.12), ни одна из этих групп уравнений (уравнения статики, геометрические и физические зависимости) отдельно не решается. Решение в окончательном виде на основе имеющихся математических методов получено только для ограниченного круга задач. Эти задачи рассматриваются в теории упругости. В практике проектирования большинства строительных конструкций обычно используют более простые инженерные методы определения напряжений. Из множества сооружений мы будем рассматривать только те, к которым эти методы применимы.

Инженерные методы оценки напряженно деформированного состояния основаны на геометрических допущениях (гипотезах). Вводимые гипотезы позволяют получить описание состояния бесконечного количества внутренних связей через конечное число параметров. Эти гипотезы зависят от соотношения размеров элементов сооружения.

Если какой-либо размер элемента мал по сравнению с двумя другими, как, например, в плитах, оболочках, складках, мембранах, то с большой достоверностью можно считать, что в направлении малого размера связи деформируются по линейному закону. Поэтому для тонкостенных конструкций в направлении малого размера принимается гипотеза Кирхгофа - Лява (G.R. Kirchhoff, 1824-1887, A.E.H. Love, 1863- 1940) о прямой недеформированной нормали: нормаль, перпендикулярная к срединной поверхности, остается перпендикулярной к ней в деформированном состоянии и не изменяет своей длины.

Если элементы имеют два малых размера по сравнению с третьим - это нити, стержни, то используется допущение Сен-Венана (A.G.K.Barre de Saint-Venant, 1797-1886) в направлении двух малых размеров. Оно заключается в том, что сечения плоские и перпендикулярные к оси до деформации стержня остаются плоскими и перпендикулярными к оси после его деформации и не изменяют своей формы.

Когда размеры элементов сооружения во всех направлениях одинакового порядка (такие элементы называются массивами), геометрические гипотезы ввести затруднительно. Поэтому для таких сооружений инженерный метод не применим.

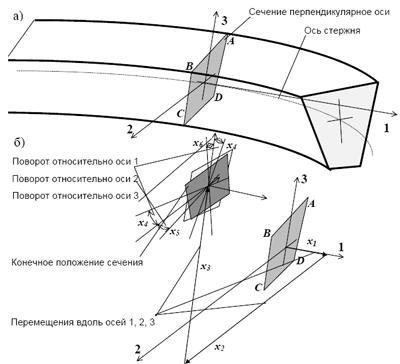
Приняв геометрические допущения, мы получаем возможность в теории тонкостенных конструкций положение всех связей определять через характеристики срединной поверхности, а в теории стержней - через характеристики оси. Гипотеза прямой недеформированной нормали позволяет деформированное ее положение определить пятью параметрами: тремя линейными (x₁ , x₂ , x₃) и двумя угловыми (x₄, x₅) (рис. 4.1). Таким образом, чтобы установить положение всех связей, достаточно знать всего пять параметров, что аналогично замене бесконечного количества микросвязей между материальными точками пятью макросвязями.

Гипотеза плоских недеформируемых сечений дает возможность определить положение сечения в деформированном состоянии стержня шестью параметрами: тремя координатами (x₁, x₂, x₃) и тремя углами поворота (x₄ , x₅ , x₆) (рис. 4.2), то есть, бесконечное количество микросвязей заменить шестью макросвязями. Если деформация стержня происходит в одной плоскости, то остается всего три параметра (три макросвязи), указывающих положение всех связей в сечении (две линейных и одна угловая).

При построении методов расчета вводится еще одно допущение геометрического характера - о малости перемещений, которое дает возможность в уравнениях статики использовать геометрические параметры (расстояния, углы), взятые в недеформированном состоянии.

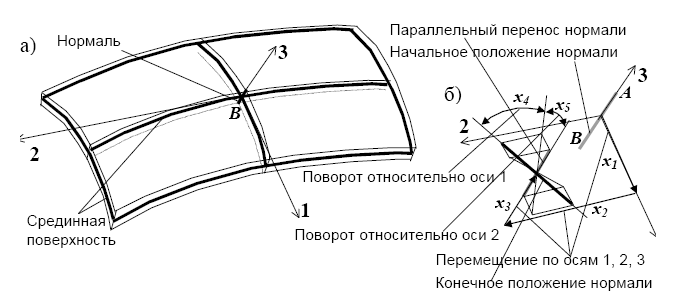
Рис. 4.1. Элемент тонкостенной конструкции (а) и перемещение нормали к срединной поверхности (б)

На основе перечисленных гипотез построены методы, позволяющие для большой группы сооружений определять внутренние усилия только из уравнений статики. Такие сооружения принято называть статически определимыми. Ниже показана методика использования статического способа на примерах плоских стержневых систем.

Рис. 4.2.Элемент стержня (а) и перемещение плоского сечения (б)

4.2. Внутренние усилия

Рассмотрим различные виды деформации прямолинейного стержня. Теория плоских сечений постулирует отсутствие давления продольных волокон друг на друга, т. е. отсутствие нормальных связей между волокнами (существуют только касательные связи), поэтому будем рассматривать стержень как множество несвязных волокон, параллельных оси.

При рассмотрении любой деформации декартовые координатные оси будем располагать так, чтобы ось z совпадала с осью стержня, а оси x и y располагались в плоскости сечения стержня перпендикулярного его оси по направлениям осей симметрии сечения, если они имеются.

4.2.1. Осевое растяжение

Рассмотрим стержень прямоугольного сечения, верхняя грань которого закреплена, а к нижней грани точно по центру сечения подвешен груз (рис.4.3). Действие груза приведет к тому, что внутренние связи начнут растягиваться (удлиняться) вдоль оси стержня z. Так как сечение плоское до деформации должно оставаться плоским, и после деформации и не должно менять свою форму, расстояние между двумя соседними сечениями l увеличится на величину Δl (рис.4.3), настолько же удлинятся и связи. Во всех других направлениях деформации отсутствуют, то есть.

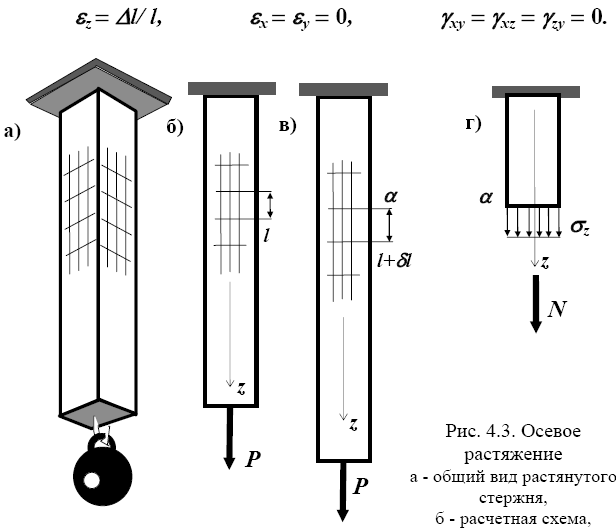
Разделим стержень сечением α на две части и рассмотрим одну из них, например, верхнюю. Придерживаясь правил принятой нами концепции сил, разорванные при этом связи необходимо заменить возникающими в них усилиями - напряжениями. По соотношению (3.10) эти напряжения будут равны

(рис.4.3). Так как деформации одинаковы, то и напряжения по сечению будут распределены равномерно, то есть σ _z = const. Следовательно, равнодействующая N напряжений σ _z должна быть приложена в центре тяжести сечения и направлена вдоль оси стержня. Эта равнодействующая называется продольной силой и значение ее равно

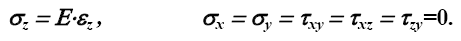
(здесь А - площадь поперечного сечения стержня).

Знак продольной силы определяется знаком σ _z (продольная сила положительна, если она растягивает стержень, и отрицательна, если его сжимает).

4.2.2. Чистый изгиб

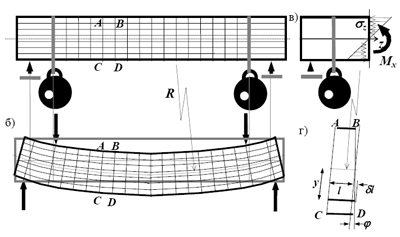
Чистый изгиб будет иметь место, если к горизонтально расположенному стержню подвесить на одинаковом расстоянии от опор два одинаковых груза, как показано на рисунке 4.4. a)

При такой деформации продольные волокна стержня будут искривляться по дуге окружности, поперечные сечения, плоские до деформации, останутся плоскими и перпендикулярными оси после деформации, но повернутся на некоторый угол φ. Длина осевых (нейтральных) волокон не изменится, нижние волокна удлинятся, а верхние укоротятся (рис.4.4). Как и при осевом растяжении, будут только продольные деформации связей. Если, учитывая гипотезу о малости перемещений, закон изменения деформаций по высоте сечения считать линейным, то относительное удлинение каждой связи будет зависеть от расстояния между нейтральным волокном и этой связью y и от изменения кривизны стержня в рассматриваемом сечении κ = φ / l .

Таким образом,
ε_z = Δl/ l =κ·y, ε_x = ε _y = 0, γ_xy = γ_xz = γ_zy = 0.

Рис. 4.4.Чистый изгиб а- схема загружения, б - схема изгибания, в - напряжения ( σ _z) и усилия (M_x ), г - элемент АВСD

Если разделить стержень любым произвольным сечением на две части и заменить разорванные связи усилиями в них (напряжениями) (рис.4.4, г), то на основании соотношения (3.10)

σ_z =Ε·ε_z= E·κ·y , σ _x = σ _y = τ_xy = τ_xz = τ_zy. (4.2)