Занятие 4. ИНЖЕНЕРНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ. ВНУТРЕННИЕ УСИЛИЯ

4.2.6. Изгиб стержня в плоскости zox

Не повторяя всех выводов для случая чистого изгиба, воспользуемся готовыми зависимостями (4.2) - (4.5) и произведем поворот осей. В любом произвольном сечении будут иметь место напряжения

σ_z = E·κ·x,

равнодействующая которых - изгибающий момент относительно оси y

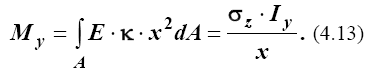
4.2.7. Изгиб в двух плоскостях (zox и zoy) с растяжением (внецентренное растяжение)

Одновременный изгиб в двух плоскостях и растяжение будем рассматривать как сумму деформаций (рис. 4.8):

- осевое растяжение (см. п. 4.2.1.), которое вызывает равномерное удлинение связей ε_z1 = Δ ₁ / l,

с равнодействующей - продольной силой

N = σ_z1 · A;

- изгиб в плоскости zoy, который характеризуется (см.п.4.2.2) удлинением связей ε_z2 = Δ₂ / l = κ _x·y, напряжениями (рис.4.8)

σ_z2 = E·κ_x·y

Рис. 4.8. Изгиб с растяжением (составляющие нормальных напряжений) а, в, д - составляющие нормальных напряжений соответственно от растяжения и изгиба в плоскостях хоz и уоz; б, г, е - внутренние усилия соответствующие растяжению и изгибу в плоскостях хоz и уоz; ж - полные напряжения; з - соответствующие им усилия; и - замена усилий равнодействующей N c эксцентриситетами

и их равнодействующей - изгибающим моментом относительно оси x

M_x = σ_z2· I_x / y;

- изгиб в плоскости zox (рис. 4.8), при котором возникают (см.п.4.2.6) деформации ε_z3 = Δ₃ / l, напряжения

σ_z3 = E·κ_y·x,

и их равнодействующая - изгибающий момент относительно оси y

M_y = σ_z3· I_y / x.

В результате сложения получаем общую деформацию

ε_z = ε_z1 + ε_z2 + ε_z3,

суммарные напряжения (рис.4.8)

σ_z = σ_z1 + σ_z2 + σ_z3

которые приводятся к трем равнодействующим

или к одной продольной силе, смещенной по отношению к центру сечения:

по оси y - на величину (эксцентриситет) e_x = M_x / N,
по оси x - на величину e_y = M_y / N,.

Для лучшего усвоения и закрепления материала рекомендуем читателю самостоятельно получить формулы внутренних усилий для следующих случаев.

4.2.8.Сдвиг с кручением (для круглого стержня) (см. рис.4.9)

Рис. 4.9. Сдвиг с кручением а, б, в - составляющие касательных напряжений соответственно от кручения и сдвига в направлении осей у и х; д, е, ж - внутренние усилия соответствующие кручению и сдвигу; г - полные напряжения; з - соответствующие им усилия; и - замена усилий равнодействующей Q = √ Q_x ² + Q_y ² c эксцентриситетом e

4.2.9. Изгиб в плоскости zoy с кручением (для круглого стержня) (для самостоятельного решения).

4.3. Статический способ определения внутренних усилий

Пусть под действием приложенной внешней нагрузки (рис.4.10) стержень находится в равновесии (дана самоуравновешенная система сил), т. е. для внешних сил выполняются условия

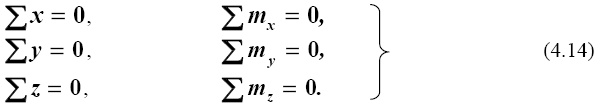
Рис. 4.10. Внутренние усилия в сечении стержня в пространстве (а) и на плоскости (б) 1 - общий вид стержня; 2- отсеченная его часть

Любая часть стержня должна находиться в равновесии под действием внешней нагрузки и внутренних усилий. Разделим стержень сечением abсd на две части. Чтобы не нарушить их равновесия, усилия в рассеченных связях заменим интегральными силовыми характе- ристиками (рис. 4.10). Ими должны быть: продольное усилие N, изгибающие моменты M_x ,M_y; крутящий момент M_z; поперечные силы Q_x, Q_y (шесть параметров соответствуют шести степеням свободы плоского сечения или шести макросвязям). Для части стержня также должны быть справедливы уравнения равновесия (4.14), но только теперь в них войдут неизвестные внутренние усилия

где P_x ,P_y, P_z - проекции приложенных к отсеченной части стержня внешних сил соответственно на оси x, y, z; M_px, M_py, M_pz - моменты внешних сил относительно осей x, y, z.

Допущение о малости перемещений дает возможность в уравнения (4.15) ввести геометрические параметры (размеры, очертания осей или углы наклона сил и их плечи) недеформированного состояния. Ввиду этого число уравнений равновесия равно числу неизвестных, система является статически определимой. При решении плоской задачи будут иметь место только три внутренних усилия (M, Q, N) и три уравнения равновесия.

Из системы (4.15) следует простой способ вычисления внутренних усилий в любом сечении свободного незамкнутого стержня, загруженного самоуравновешенной нагрузкой. Для этого необходимо провести сечение, рассмотреть любую отсеченную часть стержня и составить соответствующие уравнения равновесия.

Приведенные выше рассуждения показывают, что внутренние усилия представляют собой интегральную характеристику напряженного состояния сечения в целом, в то время как напряжения определяют состояние отдельной точки сечения. Из этих же рассуждений следует, что по известным внутренним усилиям с учетом принятых геометрических гипотез легко могут быть найдены напряжения. Внутренние усилия, таким образом, являются основным инструментом анализа напряженного состояния конструкции. Поэтому задачу вычисления внутренних усилий в строительной механике часто называют основной.

Решение задачи определения внутренних усилий и напряжений принято представлять в виде графиков - эпюр усилий и напряжений. Они показывают значения усилий и характер их изменения по длине каждого элемента сооружения и эпюр напряжений - по сечению. Эпюры дают возможность при соответствующем опыте мгновенно оценить состояние конструкции, увидеть опасные сечения (точки), наметить при необходимости способы перераспределения внутренних усилий.

В анализе напряженно деформированного состояния элементов конструкций задача определения внутренних усилий является наиболее трудоемкой, и хотя все необходимые вычисления при этом полностью основываются на составлении уравнений равновесия, для ее успешного решения требуется иметь прочные практические навыки. В связи с этим мы сочли целесообразным разделить задачу на отдельные простейшие этапы и подробно разобрать их в Приложении к настоящему курсу.

4.4. Определение напряжений по внутренним усилиям

Если внутренние усилия известны, то на основе зависимостей (4.1) - (4.12.) можно осуществить переход к напряжениям. Формулы определения напряжений по внутренним усилиям для наиболее часто встречающихся видов деформации сведем в таблице 4.4.

Таблица 4.4 Формулы для определения напряжений в поперечном сечении стержней

Вид напряженного состояния	Нормальные напряжения σ	Касательные напряжения τ
1.Центральное растяжение или сжатие		нет
2.Чистый изгиб в плоскости zoy в плоскости zox в двух плоскостях (косой чистый изгиб)		нет нет нет
3.Сдвиг (срез)	нет
4.Кручение круглого стержня	нет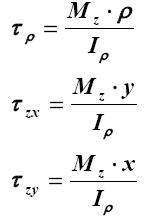
5.Поперечный изгиб в плоскости zoy в плоскости zox в двух плоскостях (косой изгиб)
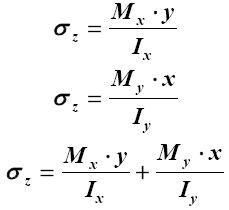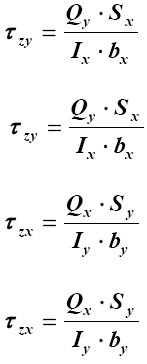6.Чистый изгиб в плоскости zoy с кручением (для круглого стержня)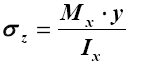
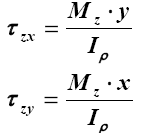7.Сдвиг с кручением (для круглого стержня)	нет
8.Косой изгиб с растяжением (сжатием) - косое внецентренное растяжение (сжатие)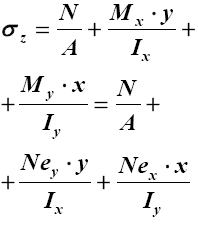
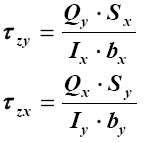9.Поперечный изгиб круглого стержня в плоскости yoz с кручением
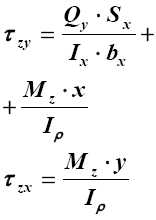Примечание. При определении напряжений для сложных напряженных состояний, так же как при выводе прямых формул определения внутренних усилий по напряжениям, используется принцип суперпозиции (принцип независимости действия сил), поэтому все недостающие формулы легко получить самостоятельно, разложив предварительно сложное напряженное состояние на простые составляющие. Этот прием, кроме того, позволит во всех случаях довольно просто определять положение опасных точек в сечении.