Занятие 5. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ. БАНК ПРЕДЕЛЬНЫХ ХАРАКТЕРИСТИК
Скачать:
П р и м е р ы 5.6-5.10 (для самостоятельного решения). Определить при внецентренном растяжении предельные продольные силы и изгибающие моменты для стержней с сечениями, представленными на рисунке 5.5.
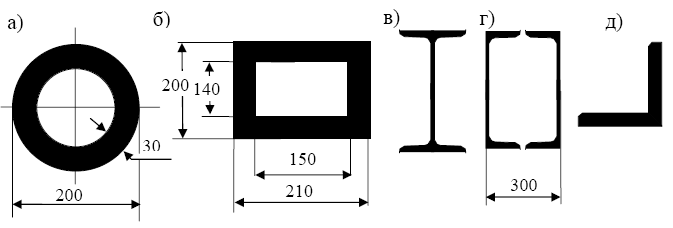
Рис. 5.5. Поперечное сечение стержней а - кольцевое, б - коробчатое, в - двутавр № 20, г - коробчатое из швеллеров № 24, д - уголковое из уголка 100х10
5.3. Формирование банка предельных нагрузок
Опорной базой в оценке прочности по нагрузке является все сооружение в целом. Ввиду широкого разнообразия сооружений, сечений их элементов, материалов и самих нагрузок составление банка предельных нагрузок - трудоемкая и трудно выполнимая, особенно экспериментальным путем, задача. Этот банк главным образом составляется теоретически по известным банкам предельных напряжений и усилий. Но если такой банк имеется, то оценка прочности и проектирование существенно упрощаются. Важно также то, что оценивается прочность всего сооружения.
П р и м е р 5.11. Составить банк предельных нагрузок для балок пролетом 6 м, выполненных из стальных двутавров по ГОСТу 8239-72, сталь марки Ст3. Нагрузка равномерно распределена по всей длине (рис.5.6). Прогиб балки не должен превышать шести сантиметров (1/100 от пролета).
Р е ш е н и е. Рассмотрим двутавр высотой h с моментом инерции I . Так как сечение по длине стержня не меняется, наиболее опасным будет сечение с максимальным изгибающим моментом. В балке, загруженной по всему пролету распределенной нагрузкой, такой момент будет в середине пролета
Mх при z=l/2 = ql2/ 8
где q - интенсивность нагрузки, l - пролет балки.
Максимальные нормальные напряжения возникают в крайних (верхних и нижних) волокнах сечения и равны
σ z max = Mх h/(2Ix>).
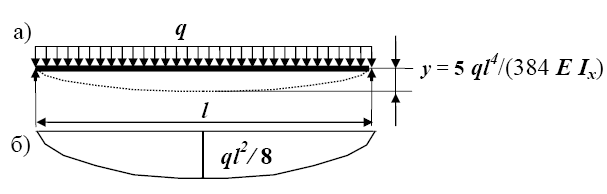
Рис. 5.6. Расчетная схема балки и эпюра изгибающих моментов к ней
Максимальный прогиб будет так же в середине пролета
y = 5 ql4/(384 E Ix),
где E = 200 ГПа - модуль упругости стали.
Предельный прогиб ynp = l /100. Из условия жесткости
y ≤ ynp получим 5 ql4/(384 E Ix) ≤ l /100
откуда предельная нагрузка по условию ограничения прогиба 1/100 пролета составит
qnp ж = 3,84 E Ix,/(5 l3) = 0.768 E I,x/ l3 (5.7)
Условие прочности σ z max ≤ Rnp, при подстановке в него напряжения, выраженного через изгибающий момент M, который в свою очередь зависит от нагрузки, преобразуется к виду
ql2 h / (16Ix) ≤ Rnp.
Откуда предельная нагрузка по условию прочности
qnp n ≤ 16RnpIx / (l2 h), (5.8)
где Rnp = 270 МПа (см. табл. 5.1).
Из двух значений нагрузок, получаемых из условий жесткости (5.7) и прочности (5.8), выбирается меньшая.
Для получения численных значений предельной нагрузки преобразуем выражения (5.7) и (5.8), подставив в них известные величины, не зависящие от размеров двутавра. Тогда уравнение (5.7) примет вид (E = 200 ГПа,. l = 6 м), если Ix измеряется в м4
qnp ж = 0.768EIx/l 3 = 0.768 ·2·1011Ix/63 = 0.0711·108Iх, (5.9)
или qnp
ж = 0.0711Iх, если Ix измеряется в см4, а уравнение (5.8) - вид
qnp
n = 16RnpIx / (l2 h) = 1.2 Iх /h. (5.10)
где Rпр = 27000 кПа , Ix измеряется в см4, h в см
Если в полученные формулы (5.9) и (5.10) подставить момент инерции Iх в см4, а высоту h в см (см. ГОСТ 8239-89, помещенный в табл. 4.2), то нагрузку qпр получим в Н/см, а чтобы перевести ее в привычную размерность кН/м необходимо ее в 10 раз уменьшить. Вычисления предельной нагрузки сведены в таблицу 5.9.
П р и м е р 5.12 (для самостоятельного решения). Построить банк данных по нагрузке (в зависимости от пролета) для черепных брусков кровли из условий прочности и жесткости. Черепные бруски сечением 5х5 см выполнены из сосны второго сорта с расчетным сопротивлением изгибу R = 7 МПа. Допустимый прогиб 1/50 от пролета.
Приведем справочные данные1 для вычислений. Расчетная схема черепного бруска - двухпролетная балка с шарнирными опорами по концам и в середине. На средней опоре такой балки изгибающий момент равен ql2 /8, момент в середине пролета - ql2 /16. Прогиб в середине пролета ql4 /(192EI).
Таблица 5.9 Предельные нагрузки для балки из двутавров по ГОСТу 8239-72 (материал - сталь Ст3)
| Номер двутавра | Высота h, см | Момент инерции Iх см4 | qnp ж, Н/см | Iх / h, см3 | qnp n, Н/см | Предельная нагрузка qпр, Н/см (кН/м) |
|---|---|---|---|---|---|---|
| 10 | 10 | 198 | 14.1 | 19.8 | 23.8 | 14.1 (1.4) |
| 12 | 12 | 350 | 24.9 | 29.16 | 35.0 | 24.9 (2.5) |
| 14 | 14 | 572 | 40.7 | 40.85 | 49.0 | 40.7 (4.1) |
| 16 | 16 | 873 | 62.1 | 54.56 | 65.5 | 62.1 (6.2) |
| 18 | 18 | 1290 | 91.7 | 71.70 | 86.0 | 86.0 (8.6) |
| 20 | 20 | 1840 | 130.8 | 92.0 | 110.4 | 110.4 (11.0) |
| 22 | 22 | 2550 | 181.3 | 115.9 | 139.1 | 139.1 (13.9) |
| 24 | 24 | 3460 | 246.0 | 144.2 | 173.0 | 173.0 (17.3) |
| 27 | 27 | 5010 | 356.3 | 185.6 | 222.7 | 222.7 (22.3) |
| 30 | 30 | 7080 | 503.5 | 236.0 | 283.2 | 283.2 (28.3) |
| 33 | 33 | 9840 | 699.7 | 298.2 | 357.8 | 357.8 (35.8) |
| 36 | 36 | 13380 | 951.5 | 371.7 | 446.0 | 446.0 (44.6) |
| 40 | 40 | 19062 | 1355.5 | 476.6 | 571.9 | 571.9 (57.2) |
| 45 | 45 | 27696 | 1969.5 | 615.5 | 738.6 | 738.6 (73.9) |
| 50 | 50 | 39727 | 2825.0 | 794.5 | 953.4 | 953.4 (95.3) |
| 55 | 55 | 55962 | 3979.5 | 1017.5 | 1221.0 | 1221.0 (122.1) |
| 60 | 60 | 76806 | 5461.8 | 1280.1 | 1536.1 | 1536.1 (153.6) |
К списку публикаций в разделе
