Занятие 5. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ. БАНК ПРЕДЕЛЬНЫХ ХАРАКТЕРИСТИК
Скачать:
Таблица 5.8 Нормативные предельные усилия стальных канатов типа ТК 7*37 с металлическим сердечником (ГОСТ 3068-80)
| Диаметр каната, мм | Площадь поперечного сечения, см2 | Предел прочности проволоки, МПа | ||
|---|---|---|---|---|
| 1700 | 1800 | 1900 | ||
| Разрывное усилие каната в целом, кН | ||||
| 21.0 | 2.045 | 284.5 | 301.5 | 318.0 |
| 23.5 | 2.473 | 344.0 | 364.5 | 384.5 |
| 25.5 | 2.940 | 409.5 | 433.5 | 457.5 |
| 27.5 | 3.452 | 480.5 | 509.0 | 537.5 |
| 29.5 | 4.004 | 558.0 | 590.5 | 623.5 |
| 31.5 | 4.580 | 637.5 | 675.0 | 712.5 |
| 34.0 | 5.224 | 728.0 | 770.5 | 813.5 |
| 36.0 | 5.898 | 820.0 | 869.0 | 918.0 |
| 38.0 | 6.598 | 918.0 | 971.5 | 1025.0 |
| 42.0 | 8.156 | 1135.0 | 1200.0 | 1265.0 |
| 45.5 | 9.906 | 1375.0 | 1455.0 | 1540.0 |
| 50.5 | 11.733 | 1630.0 | 1730.0 | 1820.0 |
| 55.0 | 13.782 | 1915.0 | 2030.0 | 2140.0 |
| 59.0 | 15.960 | 2220.0 | 2350.0 | 2480.0 |
| 63.0 | 18.345 | 2555.5 | 2705.0 | 2855.0 |
| 67.5 | 20.859 | 2905.0 | 3075.0 | 3250.0 |
П р и м е р 5.2. Определить предельную сжимающую силу для колонны трубчатого сечения. Труба из стали 10Г2АФ внешним диаметром D = 500 мм и толщиной стенки 6 мм (внутренний диаметр d = 488 мм). Длина стержня, защемленного в фундаменте, равна трем метрам.
Р е ш е н и е. Сначала определим предельно допустимое напряжение. Оно зависит от гибкости (см. табл. 5.6). (Формулу вычисления радиуса инерции см. табл.4.1).
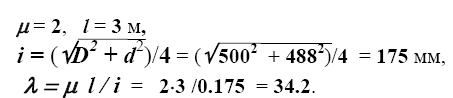
При гибкости λ = 34.2 и Rр = 400 МПа расчетное сопротивление Rпр = 352 МПа (см. табл.5.5), поэтому
Nпр = Rпр A = Rпр π(D 2 – d 2)/4 =
= 352(5002 + 4882)/4 = 3.278 МН = 3278 кН.
П р и м е р 5.3. Определить предельно допустимые усилия во внецентренное растянутом (сжатом) в вертикальной плоскости стержне, изготовленном из материала с расчетным сопротивлением R .
Р е ш е н и е. Максимальные нормальные напряжения при внецентренном действии усилий определяются по формуле (см.табл.4.2)
σ = N / + (M / I) ymax ,
из которой, обозначив W = I/ ymax - момент сопротивления, и M / N = e - эксцентриситет, получим
σ = N / A (1 + e A / W). (5.4)
По условию прочности
σmax ≤ Rпр,
следовательно, учитывая, что ARnp = N .
N ≤ Nnp / (1 + e A / W),
N ≤ Nnp α , (5.5)
где Nnp - предельно допустимое усилие при центральном растяжении (сжатии); α = (1 + e A / W) -1 - коэффициент, учитывающий внецентренное приложение нагрузки. Изменение этого коэффициента в зависимости от e A / W показано на рисунке 5.4.
При изгибе (без продольной силы) в формуле (5.5) необходимо эксцентриситет e устремить к бесконечности, но тогда смысл сравнения пропадает, так как оно покажет только то, что продольная сила равна нулю. Чтобы выйти из этого положения, формулу для максимального напряжения запишем в виде
σ = (1 + W / e A)(M/ W).
Из условия прочности, учитывая, что σmax W = Mпр, получим
M ≤ Mпр/(1 + W / e A) (5.6)
где Mпр - предельный изгибающий момент при чистом изгибе, β = (1 + W / e A) коэффициент, учитывающий наличие продольной силы. (см. рис. 5.4, β = 1 − α).
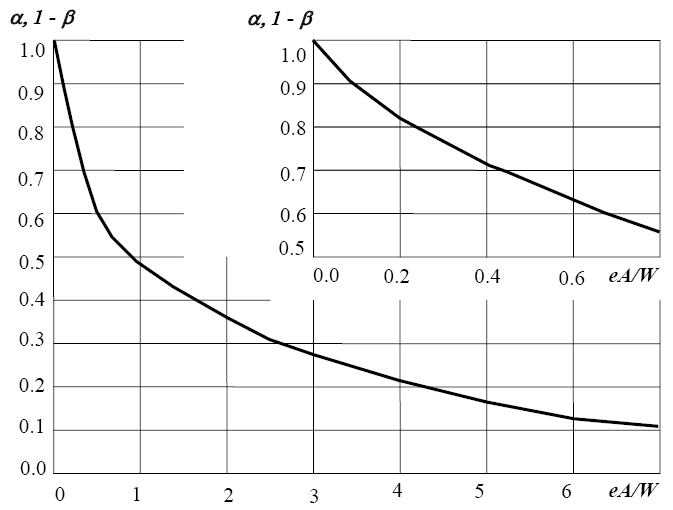
Рис. 5.4. Значения коэффициентов предельной продольной силы и изгибающего момента при внецентренном растяжении (сжатии)
П р и м е р 5.4 (для самостоятельного решения). Определить предельное усилие для чистого среза при заданном предельном напряжении Rпр.
Ответ: Qпр = Rпр A.
П р и м е р 5.5 (для самостоятельного решения). Найти предельную сжимающую силу для стержня длиной 4 м коробчатого поперечного сечения с внешней стороной a =200 мм и толщиной стенки 10 мм, выполненного из стали Ст3. Стержень свободно оперт по концам.
Ответ: Nпр = 1554 кН.
К списку публикаций в разделе
