Занятие 2-1. ВНЕШНИЕ СИЛЫ

Такими средами являются, например, жидкости и газы. Вода и газ практически не сопротивляются сдвигу, то есть в них отсутствует трение. Поэтому их давление всегда перпендикулярно поверхности.

П р и м е р 2.9. Определить давление сухого песка на подпорную стенку и построить эпюру распределения давления по высоте. Схема стенки показана на рисунке 2.13. Принять φ ₀ = 0.

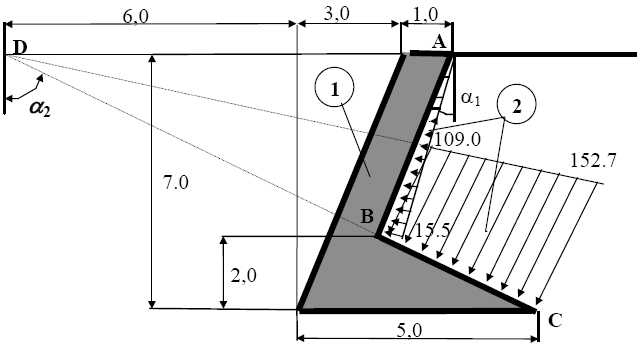
Рис. 2.13. Наклонная подпорная стенка (1) и эпюра давления сыпучего тела на нее (2) (размеры даны в м, ординаты эпюры давления - в кПа)

Р е ш е н и е. Напорная грань стенки имеет излом на ребре B, поэтому давление будем определять на каждом участке в отдельности.

Участок AB.
Определим угол наклона напорной грани ограждения

α = - arctg(3/7) = - 23,2⁰ .

Из таблицы 2.5 γ = 16 кН /м3, φ = 30⁰ .
По формулам таблицы 2.6 (схема 2)

κ = (tg(45⁰ - (30⁰ +23.2⁰)/2) - 3/7)² cos23.2⁰ = 0.194.

Интенсивность давления

в точке A (h = 0) q = 0,
в точке B (h = 5) q = γhκ = 16·5·0.194 = 15.5 кПа.
Участок BC.

Для определения давления на грань BC образуем фиктивную напорную грань CD и рассчитаем давление на нее, а затем оставим только то давление, которое приходится на грань BC.

Угол наклона грани
α = - arctg(11/7) = 57.5⁰ .
По формулам таблицы 2.6
κ = (tg(45⁰ - (30⁰ -57.5⁰)/2) - 3/7)² cos57.5⁰ = 1.363.

Давление на грани BC
в точке B (h = 5) q = 16·5·1.363 = 109.0 кПа,
в точке C (h = 7) q = 16·7·1.363 = 152.7 кПа.
Эпюры давления построены на рисунке 2.13.

П р и м е р 2.10. Определить давление гравийного грунта на вертикальную стенку. Высота стенки 5 м. На глубине 3 м обнаружена грунтовая вода (рис.2.14).

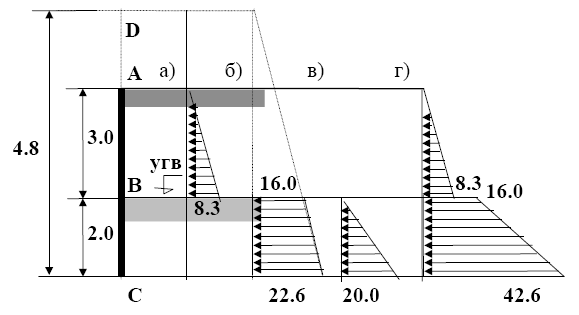
Рис. 2.14. Давление грунта, насыщенного водой:
а - эпюра давления на грань АВ; б – то же на грань DС; в - давление воды; г - суммарная эпюра давления воды и грунта (размеры даны в м, давление - в кПа)

Р е ш е н и е. Сначала определим давление сухого гравия на грань AB (γ = 16 кН/м³, φ = 45⁰ из табл. 2.6)

q = 0,
q = γ·h·κ = γ·h·tg (45⁰ - φ/ 2) = 16·3·tg (45⁰ - 45⁰/2) = 8.3 кПа.

Ниже уровня грунтовых вод гравий находится в воде и теряет в весе столько, сколько воды вытесняется его частицами. Так как удельный вес грунта полностью насыщенного водой (табл. 2.5) γ = 20 кН/м3, а сухого γ = 16 кН/м³, то с учетом взвешивающего действия (γ _воды = 10 кН/м³) воды удельный вес грунта в воде вычислим из следующих соображений.

Пусть объем сухих частиц в одном кубометре составляет V_частиц. Тогда его величину в единице объема грунта можно определить из соотношения

(1- V_частиц.) 10 + 16 = 20,

 откуда V_частиц = 0.6, и поэтому удельный вес взвешенного в воде грунта равен γ_{грунта в воде} = 16 - 0.6·10 = 10 кН/м³

Таким образом, грунт за стенкой имеет разный объемный вес (16 кН/м³ вверху и 10 кН/м³ внизу) и разные углы внутреннего трения (вверху φ = 45⁰ , внизу φ = 30⁰). Чтобы привести их к однородному по объемному весу, увеличим высоту верхнего слоя (см. (2.3)) на

h_экв = h γ /γ _экв= 3·16/10 = 4.8 м.

Определим давление на ограждение высотой 2 + 4.8 = 6,8 м (DC на рис. 2.14). Кроме того, изменим угол φ = 30⁰, тогда

q = γ·h·κ = γ·h ·tg² (45⁰ - φ / 2) = 10·6.8·0.333 = 22.6 кПа,
q = 10·4.8·0.26 = 16.0 кПа

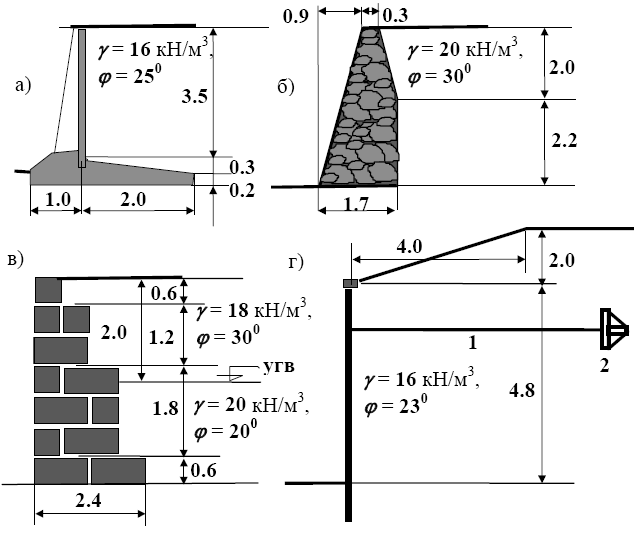
Рис.2.15.Подпорные стенки и характеристики засыпки:
а - железобетонная уголковая стенка, б - бутовая стенка, в - стенка из фундаментных блоков, г - шпунтовая стенка (больверк); 1 - анкерная тяга, 2 - анкер

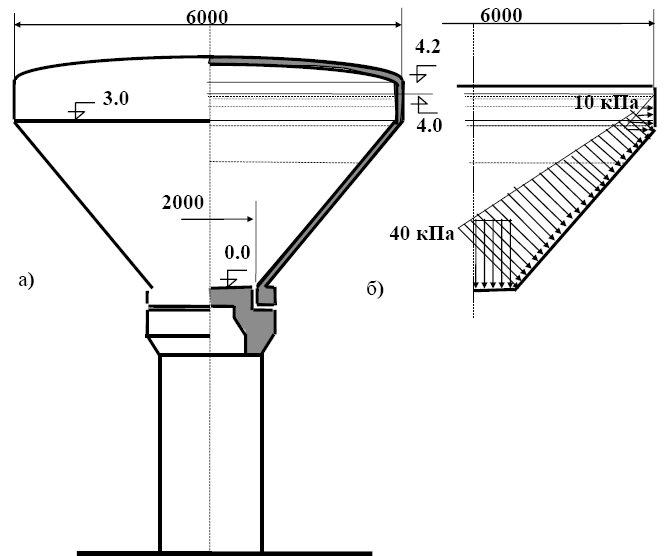
Рис.2.16. Железобетонная водонапорная башня
а - фасад башни с разрезом, б - эпюра давления воды на стенки резервуара и днище

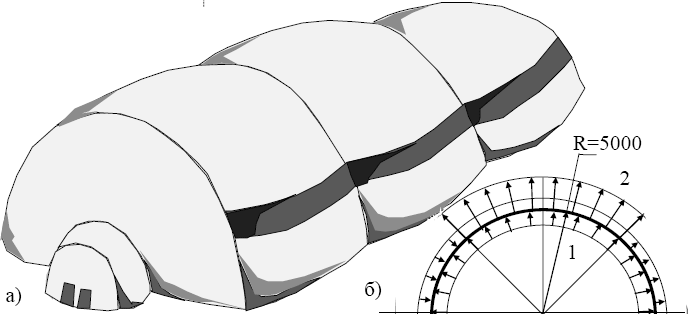
Рис.2.17. Воздухоопорный склад
а - общий вид склада; б - нагрузка на оболочку; 1 - избыточное внутреннее давление; 2 - ветровая нагрузка (ветер слева)