Занятие 2-1. ВНЕШНИЕ СИЛЫ
Скачать:
Таблица 2.1
Средние удельные веса распространенных строительных материалов (γ, кН/м3)
| Материал | γ | Материал | γ |
|---|---|---|---|
Гранит |
21 |
Пенопласт |
2 |
| Примечание. Удельные веса сыпучих тел (грунтов) см. таблицу 2.5 | |||
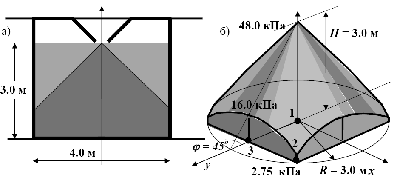
Рис.2.3. Банка склада инертных материалов а - разрез банки, б - Форма насыпи в ней
Р е ш е н и е. Наибольшее давление на пол будет в том случае,
когда банка будет загружена полностью равномерным слоем высотой 3 м.
При удельном весе сухого гравия γ = 16 кН/м3 (см. табл. 2.5) будем
иметь интенсивность давления
q = 16·3 = 48 кН/м2.
Замечание 2. Однако, реализовать такое давление по всей площади при одном бункере в середине банки очень трудно без дополнительных работ по разравниванию гравия. При заполнении банки через бункер, вероятнее всего, будет образован конус с вершиной в уровне низа бункера, т. е. высотой три метра. Чтобы ответить на вопрос о том, как изменится давление на пол банки, если учесть наиболее вероятное ее заполнение через центральный бункер, мы должны получить закон распределения высоты слоя по площади пола, который совпадает с уравнением поверхности конуса в координатах x, y, z (см. рис. 2.2). Угол естественного откоса гравия по таблице.2.5 равен 45о. Поэтому радиус основания конуса должен быть равен его высоте, то есть R = 3 м. Но полностью такой конус в банку не помещается. Поэтому он будет не полным (см. рис. 2.2). Уравнение поверхности конуса 3
h = z = H (1 - √ x2 + y2 / R),
или с учетом того, что H = R = 3 м
h = 3 - √ x2 + y2.
Давление на пол определим в характерных точках по формуле (2.2):
точка 1 (x = 0, y = 0) q = 16·3 = 48 кН/м,
точка 2 (x = 2, y = 2) q = 16·(3 - √ 22 + 22) = 2,75 кН/м,
точка 3 (x = 2, y = 0) q = 16·(3 - √ 22 + 22) = 16 кН/м.
Таким образом, пол банки будет загружен неравномерно. В углах давление приближается к нулю, в середине каждой стороны оно в три раза меньше, чем от равномерно распределенного слоя. Банка заполняется всего на половину своего объема. Чтобы использовать более полно объем банки, в ее перекрытии можно установить большее количество бункеров (например, четыре) или загрузить материалом с меньшим углом внутреннего трения (например, углом внутреннего трения 25о). Определить величины давления и оценить неравномерность загрузки банки в этих случаях читатель может самостоятельно.
Собственный вес конструкции также можно отнести к однородной гравитационной среде. Усредненная поверхностная нагрузка может быть определена делением собственного веса изделия на горизонтальную проекцию его поверхности
q = G/A. (2.3)
Эта усредненная поверхностная нагрузка может использоваться в качестве нагрузки рабочего состояния тем точнее, чем меньше изменение высоты изделия по площади за счет ребер, отверстий и других возмущений.
П р и м е р 2.2. Определить среднюю интенсивность поверхностной нагрузки от плиты покрытия, выполненной из тяжелого железобетона и имеющей размер в плане 3×6 м. Объем плиты 1.15 м3 (рис.2.3).
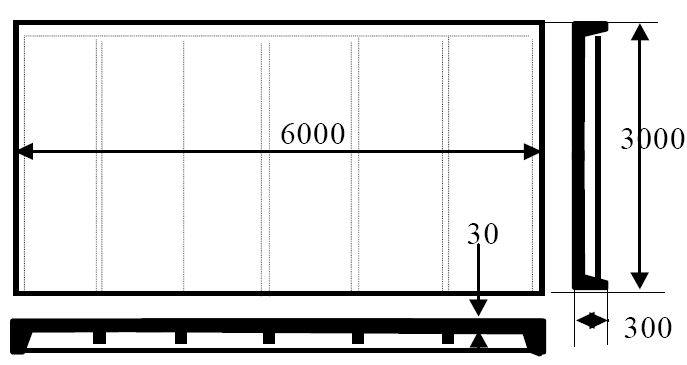
Рис. 2.3.Плита покрытия
Р е ш е н и е. Удельный вес тяжелого железобетона 25 кН/м3 . Вес плиты G = V·γ = 1.15·25 = 28.75 кН. Усредненная нагрузка от плиты
q = G/A = 28.75/(3·6) = 1.597 кН/м2.
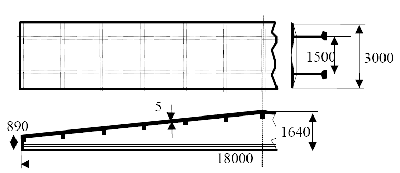
П р и м е р 2.3 (для самостоятельного решения). Плита покрытия ТТ (два ТЭ) имеет размеры в плане 3×18 м. Определить среднюю нагрузку от собственного веса плиты, если она выполнена из конструкционного керамзита. Объем плиты 3.56 м (рис.2.4).
Рис. 2.4. Плита типа ТТ (два ТЭ)
Слоистая среда образуется напластованием материалов, отличающихся плотностью и, следовательно, удельным весом γ. Формула (2.2) в чистом виде применяется только к одному слою. Давление же всех слоев равно сумме давлений каждого из них, то есть
где n - количество слоев.
Иногда слоистая среда приводится к однородной среде. Операция приведения напластования к однородному слою заключается в том, что один из них выбирается за основу для приведения (γ экв), а затем из условия равенства давлений hi · γi = hэкв ·γэкв определяется высота эквивалентного слоя
hiэкв = hi · γι / γ экв . (2.5)
Высота однородного слоя определяется как сумма эквивалентных слоев.
П р и м е р 2.4. Определить давление на перекрытие от пола и несущей плиты. Пол выполнен из дубового паркета. Толщина его 2 см. Паркет укладывается по черному полу из сосны (толщина 5 см). Черный пол устроен по лагам 5×8 см с шагом 60 см. Лаги утоплены в звукоизоляционный шлакобетонный слой толщиной 8 см. Железобетонная несущая плита имеет высоту 12 см.
Р е ш е н и е. Слоистое перекрытие имеет различные по высоте удельные веса материалов. Для определения нагрузки от каждого слоя будем использовать зависимость (2.2), а затем полученные значения просуммируем (табл.2.2).
Таблица 2.2 Нагрузка от перекрытия
| Состав перекрытия | Толщина, см | Удельный вес, кН/м 3 | Вес слоя, кН/м 2 |
|---|---|---|---|
| Пол паркетный | 2 | 8 | 0,16 |
| Черный пол | 5 | 5 | 0,25 |
| Слой шлакобетона с втопленными лагами | 8 | 13.25 | 1.06 |
| Плита перекрытия | 12 | 25 | 3.0 |
| Итого | 4,47 |
К списку публикаций в разделе