Занятие 2-1. ВНЕШНИЕ СИЛЫ
Скачать:
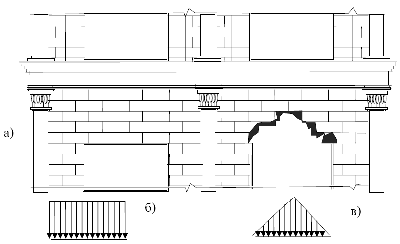
Замечания по модели разрушения гравитационной нагрузки. Отметим, однако, что гипотеза об отсутствии горизонтальных связей в материале при нахождении величины гравитационной нагрузки не всегда оправдана и приводит к существенному завышению нагрузки. Особенно это показательно в том случае, когда высота столба материала соизмерима с размерами несущей конструкции, на которую передается его вес (рис.2.10, 2.11).
Примером такой нагрузки является давление высокой кладки на перемычку оконного или дверного (оконного) проема. Повседневная практика позволяет относительно точно представить картину разрушения: при удалении перемычки разрушится только часть кладки (см. рис.2.10). При этом образуется некоторый свод с передачей нагрузки на опоры, а на перемычку будет оказывать давление только разрушившаяся часть кладки.
Рис. 2.10. Разрушение стены над перемычкой нижнего этажа (а) палаццо Ручелаи (Венеция) и схема нагрузки на нее по гипотезе разрушения гравитационной среды (б) и загружение от веса выпавшей кладки (в)
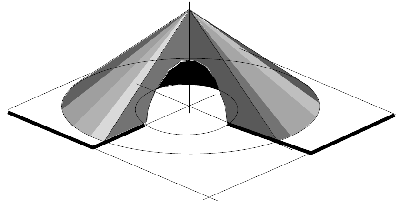
Рис.2.11. Потерна над отверстием в насыпи гравия - свидетельство условности гипотезы разрушения гравитационной среды
Несмотря на недостатки гипотеза разрушения, принятая в теории давления гравитационной среды, в большинстве случаев вполне приемлема и широко используется на практике.
2.3. Боковая нагрузка от несвязных сред
Хотя причиной бокового давления является та же тяжесть, но ввиду отличия гипотезы разрушения от той, которая была рассмотрена ранее - при вычислении гравитационной нагрузки, мы разберем эту нагрузку отдельно.
Одним из примеров несвязных сред может выступать сыпучее тело - грунт, зерно и др. Оно представляет собой совокупность твердых частиц, сцепление между которыми незначительно. Сыпучее тело сохраняет свою форму лишь в том случае, если оно ограничено так называемым углом естественного откоса (углом внутреннего трения). Поэтому если сыпучее тело засыпано в сосуд, оно является причиной давления не только на горизонтальную, но и на вертикальную (наклонную) поверхность или причиной бокового давления.
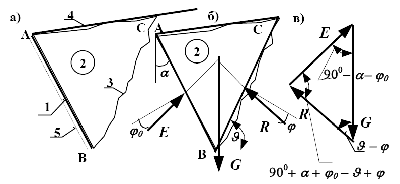
Схему разрушения несвязного тела можно представить, если перемещать ограждение в сторону от засыпки (рис.2.12). Как показывает опыт, от сыпучего тела отделится некоторая часть ABC, которая сползает по некоторой поверхности BC и поверхности ограждения AB. Кривизна поверхности BC незначительна и ее можно считать плоскостью. Поэтому поверхность BC называют плоскостью обрушения, а часть сыпучего тела ABC - призмой обрушения (высота призмы - в направлении перпендикулярном плоскости чертежа).
Таблица 2.5 Средние углы внутреннего трения и удельные веса грунтов и пшеницы
| Наименование сыпучего тела | Удельный вес, кН/м3 | Угол внутреннего трения, градусы |
|---|---|---|
| Песок сухой | 16 | 30 |
| Песок влажный | 18 | 40 |
| Песок мокрый | 20 | 25 |
| Глина сухая | 16 | 40 |
| Глина мокрая | 19 | 20 |
| Гравий сухой | 16 | 45 |
| Гравий мокрый | 20 | 30 |
| Галька | 18 | 30 |
| Пшеница | 7.5 | 30 |
Рассмотрим момент начала сползания, когда связи между грунтом и ограждением еще существуют, но напряжение в них максимально. К этому случаю могут еще применяться условия равновесия. Поэтому выделим призму обрушения и заменим действие отброшенных связей равнодействующими: E - в связях между ограждением и телом, а R - в связях между частицами самого тела по поверхности обрушения. Из-за отсутствия сцепления и наличия только сил трения эти равнодействующие при движении должны отклониться от перпендикуляра к поверхности на соответствующий угол трения ( φо - угол трения сыпучего тела об ограждение и φ - угол внутреннего трения - значения его для некоторых материалов приведены в табл. 2.5) (см. рис. 2.12).
Рис. 2.12. Призма обрушения в сыпучем теле за подпорным сооружением
а - схема разрушения; б - силы, действующие на призму обрушения при ее сползании; в - силовой многоугольник; 1 - подпорное сооружение(ограждение), 2 - призма обрушения, 3 - поверхность обрушения, 4 - поверхность засыпки, 5 - положение напорной грани при сдвиге
Кроме реакций в связях на призму обрушения действует еще и ее собственный вес - G. Три силы E, R и G находятся в равновесии, если они пересекаются в одной точке и треугольник сил замкнут (см. рис.2.12). Для рассматриваемого момента предельного равновесия по теореме синусов (с учетом известного соотношения
![]()

Но в правую часть выражения (2.6) входит неизвестный угол ![]() который определяет и вес призмы обрушения. Поэтому Шарль Август
Кулон (C.A. Coulomb, 1736 - 1806), теорию которого мы изложили выше,
предложил вычислить угол
который определяет и вес призмы обрушения. Поэтому Шарль Август
Кулон (C.A. Coulomb, 1736 - 1806), теорию которого мы изложили выше,
предложил вычислить угол ![]() дающий максимальное давление E, то есть
ввести дополнительное условие максимума
дающий максимальное давление E, то есть
ввести дополнительное условие максимума

П р и м е р 2.8. Вывести формулу для определения давления сыпучего тела с горизонтальной поверхностью на вертикальное ограждение (α = 0). Углом трения сыпучего тела по ограждению пренебречь (φ о = 0) 4. (Мы здесь не приводим чертеж к примеру 2.8, но при необходимости его легко можно выполнить самому читателю.)
Р е ш е н и е. Давление грунта при заданных параметрах определяется по формуле (2.6)
![]()
Вес призмы обрушения равен (в направлении, перпендикулярном чертежу примем размер ее равный единице)
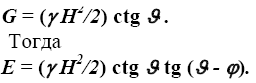
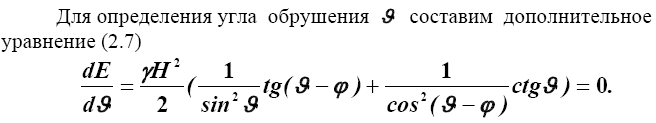
После преобразований (приведения к общему знаменателю, сокращений и замене 2 sin α·cos α на sin 2α)
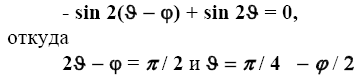
Окончательно полное давление определится по формуле
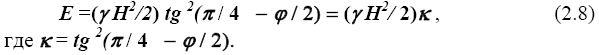
Подобным образом можно получить давление и для любого другого случая. В таблице 2.6 приведены формулы для вычисления κ в формуле (2.8) при наклонном ограждении и негоризонтальной засыпке (читатель может получить их самостоятельно).
Таблица 2.6 Давление сыпучих тел на ограждения при отсутствии трения грунта о стенку
(φ о = 0)
E = (γ H2/ 2)κ , q = γ H κ
Чтобы определить интенсивность давления сыпучего тела на поверхность, необходимо приращение силы E на высоте h отнести к приращению высоты, т. е.
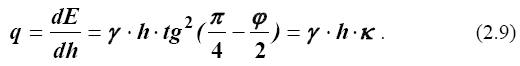
При φ = 0 получаем формулу интенсивности давления на горизонтальную, вертикальную и любую другую поверхность (q = γ·h), совпадающую с (2.2) для среды, внутри которой отсутствует трение.
К списку публикаций в разделе