Занятие 3. ВНУТРЕННИЕ СИЛЫ. НАПРЯЖЕНИЯ

Аналогично из выражения (3.4) получим уравнение

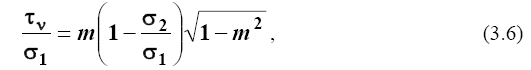
которое определяет касательные напряжения на любой площадке.

Графики, представленные на рисунке 3.4, показывают изменение нормального и касательного напряжений в масштабе σ ₁ в зависимости от направления площадки, проходящей через заданную точку. Начало координат принято в заданной точке, через нее под углом α ₁ проводится площадка ν ₁ (след ее на чертеже представляется лучом, выходящим из точки). Вектор, проведенный из начала координат до кривой τ в плоскости площадки, показывает величину и направление касательного напряжения, а вектор, проведенный от начала координат до кривой σ перпендикулярно площадке ν ₁ (перпендикулярно лучу), - величину и направление нормального напряжения. По этим графикам легко установить площадки с наибольшими напряжениями. Так, например, хорошо видно, что наибольшие касательные напряжения действуют по площадкам, расположенным под углом 45^o . Их величина вычисляется по

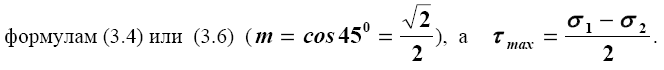
3.4. Уравнения равновесия

В уравнениях равновесия (3.1) мы не использовали три уравнения моментов относительно координатных осей. Из этих уравнений (вывод их можно найти в указанных ранее источниках) выводится закон парности касательных напряжений

С учетом (3.7) и гипотезы сплошности для каждой точки можно составить три дифференциальных уравнения равновесия (внешние гравитационные силы отсутствуют)

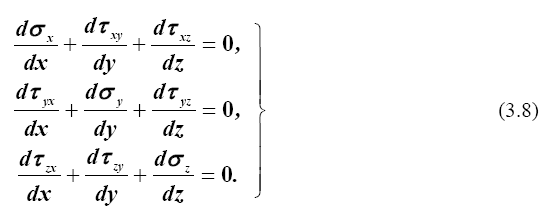
В них входят шесть непрерывных функций напряжений, то есть задача нахождения напряжений является статически неопределимой.

3.5. Физические соотношения

Так как для определения напряжений условий равновесия недостаточно, требуются дополнительные соотношения. Одни из них выведем на основании закона Гука - правила, позволяющего от удлинений в связях перейти к усилиям в них. Такие выражения носят название физических соотношений. Для традиционных строительных материалов они получены, а для новых материалов их устанавливают экспериментально. При этом свойства материалов определяют некоторые физико-механические постоянные, которые часто называют упругими постоянными. Если каждую связь или группу связей характеризовать одной постоянной, то физических уравнений получится чрезвычайно много³. Для уменьшения количества таких соотношений примем гипотезу однородности материала. Она заключается в том, что свойства связей не зависят от их положения и одинаковы во всем объеме тела - сооружения⁴. С учетом этой гипотезы и свойства идеальной упругости физико-механические свойства характеризуются тремя постоянными:

E - модулем продольной (нормальной) упругости, или модулем Юнга (T. Young, 1773-1829);

μ - коэффициентом поперечной деформации, или коэффициентом Пуассона (S.D. Poisson, 1781-1840);

G - модулем сдвига, или постоянной Ляме (G. Lame, 1795- 1870), который для упругого изотропного тела не является независимым, а связан с E и μ соотношением

При абсолютной упругости изотропного тела физические соотношения имеют вид:

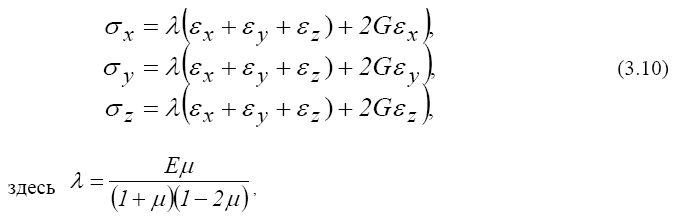
деформации ε _x, ε _y, ε _z выражают удлинения связей в направлении осей x, y, z; а γ_xy , γ_yz, γ_zx - сдвиг связей в соответствующих плоскостях xy, уz и zx.

Из соотношений (3.10) получаются зависимости деформаций от напряжений:

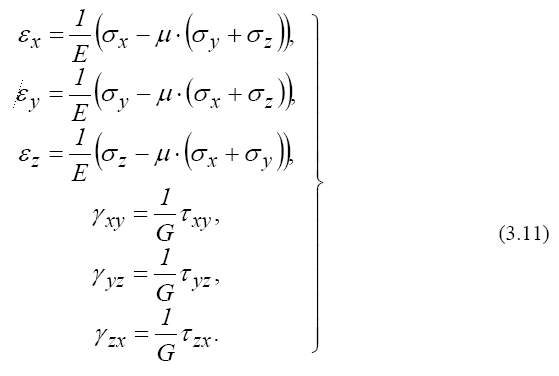
Таким образом, три уравнения равновесия (3.8) дополняются шестью физическими соотношениями (3.10), но в них входят дополнительно и шесть деформаций. Чтобы привести в соответствие количество уравнений и неизвестных, добавим еще геометрические зависимости деформаций и перемещений.

3.6. Геометрические уравнения

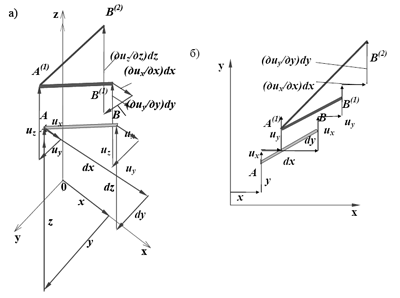
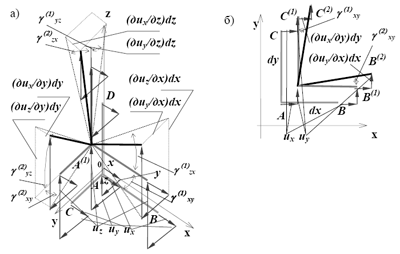
Перемещение точки определяется тремя составляющими u_x , u_y , u_z- линейными смещениями вдоль осей координат (рис.3.5). Деформации и перемещения связаны соотношениями, которые относительно просто получаются из геометрических соображений (рис. 3.5, 3.6)

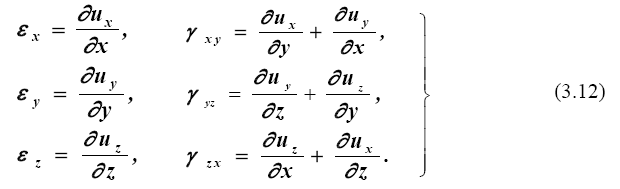
Рис. 3.5. Перемещения и удлинения связей в пространстве (а) и на плоскости (б)

В пятнадцати полученных соотношениях (уравнений равновесия (3.8) - три, геометрических уравнений (3.12) - шесть, физических (3.10) - шесть) содержится пятнадцать неизвестных (шесть компонентов напряжений, шесть компонентов деформаций и три компонента перемещений). Они составляют полную систему. В математической теории упругости доказывается, что такая система имеет единственное решение⁵. Однако математические трудности совместного решения этих уравнений до сих пор полностью не разрешимы.

Имеется небольшое количество решенных частных задач, но требованиям практики они удовлетворить не могут. Тем не менее приведенные рассуждения полезны, так как дают возможность понять физическую и математическую постановку задачи и перейти в дальнейшем к построению инженерных методов определения напряжений и основанных на них критериев прочности.