Занятие 3. ВНУТРЕННИЕ СИЛЫ. НАПРЯЖЕНИЯ

3.1. Напряжения

Уровень оценки прочности по нагрузке отличают простота и доступность. Расчеты при этом чаще всего минимальны - требуется определить только саму нагрузку. Для выполнения поверочного расчета достаточно получить навыки в определении нагрузки, пользовании банком предельных характеристик и сравнении рабочей и предельной ее величины. Проектировочный расчет на этом уровне выполняется выбором из банка данных такого сооружения, для которого допустимая нагрузка не меньше расчётной (в рабочем состоянии).

меньше расчётной (в рабочем состоянии). Навыками работы на уровне нагрузки должен обладать всякий специалист, чья деятельность в той или иной степени связана со строительством. Но если он только это и умеет, то его деятельность скована и ограничена главным образом объемом банка данных. Кроме того, нужно понимать, что по нагрузке нельзя выявить причины недоступности эксплуатации заданного сооружения в конкретных условиях. Невозможно установить, как и какими конструктивными решениями противостоять разрушению. Весьма трудно пополнить банк данных. И тем более немыслимо оценить резерв прочности в изменившихся условиях или степень использования прочностных свойств материала в отдельных частях сооружения. Невозможно оптимизировать конструктивные решения и решить целый ряд других практических инженерных задач. Это обусловлено тем, что при расчете нагрузки определяются силы во внешних по отношению к сооружению связях, само же сооружение при этом считается цельным (нерушимым) и что происходит в нем самом неизвестно. Нагрузка только способствует степени напряженности внутренних связей, несущих “полную ответственность” за сохранность сооружения. И поэтому, чтобы ставить и решать практические вопросы конструирования, необходимо изучить работу внутренних связей.

Обратимся к модели, построенной выше, согласно которой сооружение - тело, состоящее из множества бесконечно прочных частиц, соединенных между собой связями. Всякие изменения в таком теле (удлинения, деформации, разрушения) возможны только за счет изменения состояния связей.

Чтобы поставить математически и решить задачу о напряженности внутренних связей, введем гипотезы об их качестве. Будем считать, что связи заполняют тело сплошь - гипотеза сплошности. Это позволит нам рассматривать состояние сколь угодно малой частицы тела вплоть до отдельной точки и использовать для описания всего сооружения и отдельных его частей непрерывные функции. Гипотеза сплошности в подавляющем большинстве случаев отвечает реальной физической природе тел, в которых частицы (даже конечных размеров), его составляющие, малы по сравнению с размерами всего тела (сооружения).

Каждая материальная точка в сплошном теле множеством связей соединена с другими точками. Выделим мысленно одну из них. При этом мы вынуждены на основании известного из теоретической механики принципа и самой концепции сил отбросить все окружающие ее связи и заменить их действие силами. Так как любая точка в теле находится в равновесии, то мы не обнаружим этих сил. Только разделив силы на отдельные группы, мы получаем возможность их изучать. Произвольной плоскостью ν, проведенной через точку M (рис.3.1), разделим связи (силы) на две группы (связи с одной стороны от плоскости и с другой).

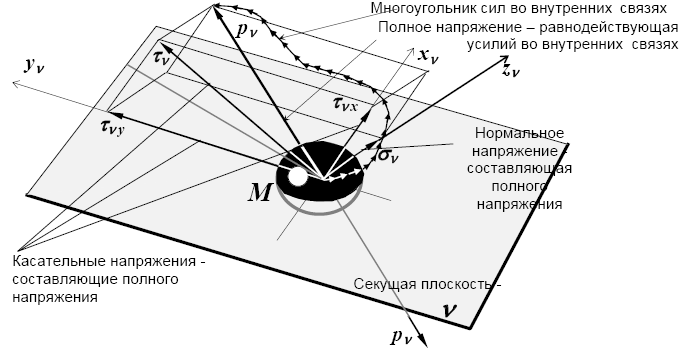
Рис. 3.1. Материальная точка М и усилия в ее связях со средой и другими точками тела

Тогда, рассматривая только одну группу сил, мы в соответствии с законами теоретической механики сможем привести их к одной равнодействующей - p_ν . Эту силу называют полным напряжением в точке для заданной площадки ν (плоскости). Полное напряжение (его направление и величина) определяется двумя компонентами - проекциями на два направления; нормальным к плоскости и касательным в самой плоскости. Касательные напряжения обычно раскладывают еще в плоскости в соответствии с выбранными осями. Компоненты полного напряжения называют соответственно нормальным -σ_ν и касательными τ_νx, τ_νy напряжениями¹. Напряжения считаются положительными, если их направления совпадают с положительным направлением осей.

С другой стороны плоскости ν (рис.3.1) действуют такие же по величине, но направленные в противоположную сторону силы - p_ν. Это автоматически вытекает из равновесия точки.

3.2. Соотношения между напряжениями на различных площадках

Прежде чем познакомиться с постановкой задачи по определению напряжений при заданной нагрузке, ответим на вопрос о том, все ли напряжения по различным площадкам являются независимыми (величина и направление полного напряжения зависит от положения плоскости ν - это очевидно). Для того чтобы на него ответить, рассмотрим равновесие точки M под действием напряжений по четырем площадкам (рис.3.2): три из них (x, y, z) взаимно перпендикулярны, а

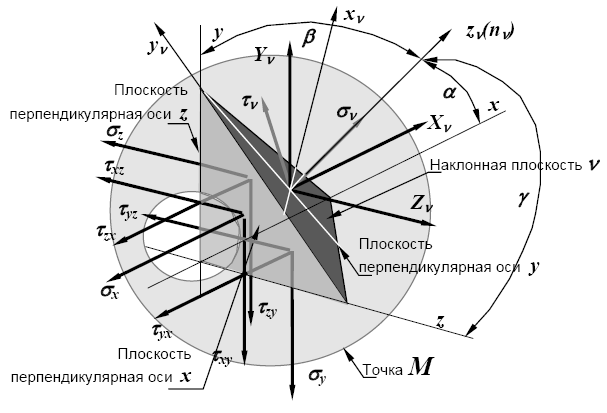
Рис. 3.2. Напряжения по трем взаимно перпендикулярным площадкам (плоскостям) и одной наклонной, проходящей через материальную точку

четвертая - ν, имеет произвольное направление, определяемое нормалью n_ν (направляющими косинусами l = cos α, m = cos β , n = cos γ). Из условий равновесия (проекций сил на оси x, y и z) получаем

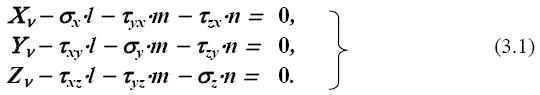
где X_ν , Y_ν , Z_ν - проекции полного напряжения на координатные оси - p²_v = Χ²_v +Υ²_v +Ζ²_v .

Из уравнений (3.1) следует, что если известны девять компонентов напряжений по трем взаимно перпендикулярным площадкам ( σ _x, σ _y, σ _z, τ_xy, τ_xz, τ_yx, τ_yz, τ_zx, τ_zy), то могут быть определены напряжения по любым другим площадкам. Проецируя найденные из этих уравнений X_ν , Y_ν , Z_ν на нормаль к плоскости - ν, получаем нормальные напряжения, а касательные напряжения определим вычитанием из полного напряжения нормальных

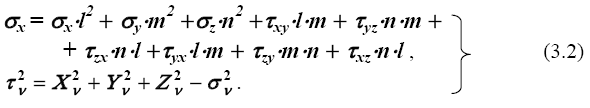
3.3. Главные напряжения

При заданных девяти компонентах первое уравнение (3.2) представляет собой поверхность второго порядка при изменении ориентации площадки (l, m, n). Ее называют поверхностью нормальных напряжений, или поверхностью Коши (A.L. Cauchy, 1789-1857). Из аналитической геометрии² известно, что путем надлежащего поворота осей координат уравнение такой поверхности может быть приведено к каноническому виду. Такое уравнение не содержит произведений направляющих косинусов². Это возможно в том случае, когда касательные напряжения на взаимно перпендикулярных площадках будут равны нулю.

Координатные оси канонической системы координат обозначим цифрами 1, 2, 3

σ_ν = σ ₁·l² + σ ₂·m² + σ ₃·n². (3.3)

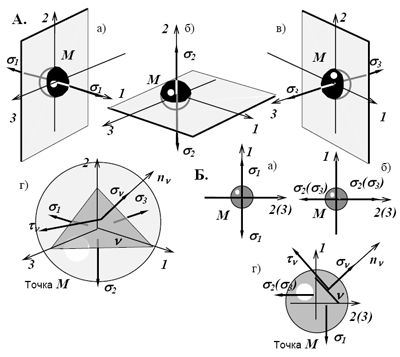
Эти площадки называют главными, а напряжения σ ₁, σ ₂, σ ₃ - главными напряжениями (рис.3.3).

Рис. 3.3.Главные площадки и главные напряжения а, б, в - главные площадки (плоскости), г - напряжения на наклонной площадке А - в пространстве, Б - на плоскости

Касательные напряжения на площадке ν также могут быть выражены через главные напряжения

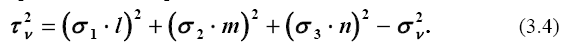
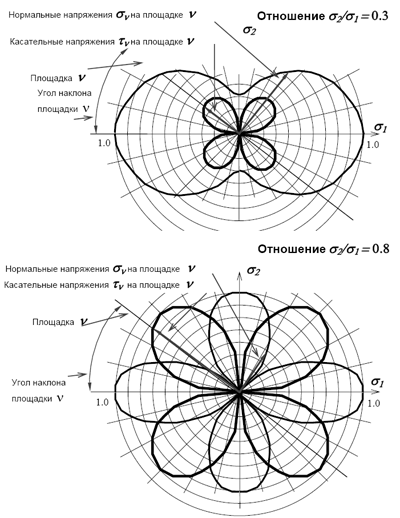
Изменение σ_ν и τ_ν в зависимости от углов наклона площадки по отношению к главным показано на графиках (рис. 3.4), построенных для случая, когда один из направляющих косинусов (например, n) равен нулю (плоская задача). Принимая во внимание, что l₂ + m₂ = 1, разделим все члены уравнения (3.3) на σ ₁. После простых преобразований получим

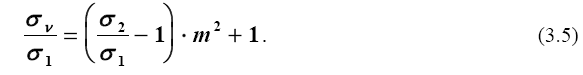
Рис. 3.4. Нормальные (тонкая линия) и касательные напряжения (жирная линия) в зависимости от наклона площадки, проходящей через точку. Напряжения отнесены к максимальному главному напряжению, минимальное главное напряжение равно нулю

Пользуясь уравнением (3.5), можно легко найти значение σ_ν при заданных σ ₁ и σ ₂ . Напомним, что m - косинус угла между нормалью к площадке и осью 2 координат.