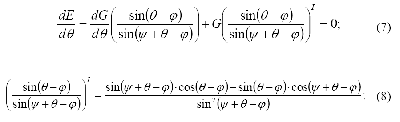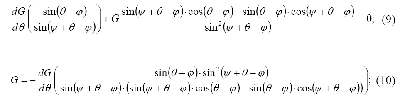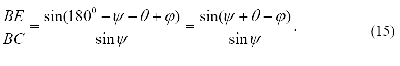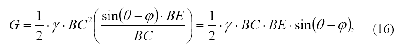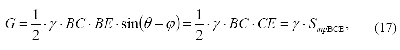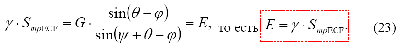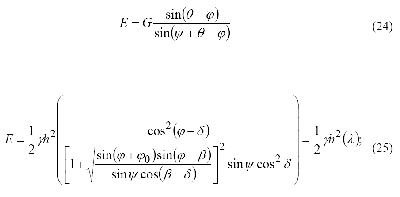Занятие 3. МЕТОДИКА РАСЧЕТА ДАВЛЕНИЯ СЫПУЧЕГО ТЕЛА НА ОГРАЖДЕНИЯ

ТЕОРЕМЫ РЕБХАНА

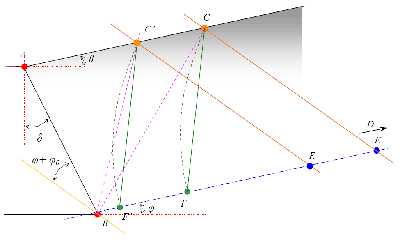
Несколько интересных работ в направлении развития теории Кулона выполнены Георгом Ребханом (рис. 1, б).

Мы остановились на том, что уравнение определения давления сыпучего тела на ограждение содержит неизвестный угол θ, который определяет также и вес призмы обрушения G. То есть θ является единственной независимой переменной в этой формуле. Ш. Кулон предложил принять угол наклона плоскости скольжения таким, чтобы активное давление на стену было наибольшим. Задача решается перебором, но более обоснованно её можно решить, введя недостающее уравнение (3).

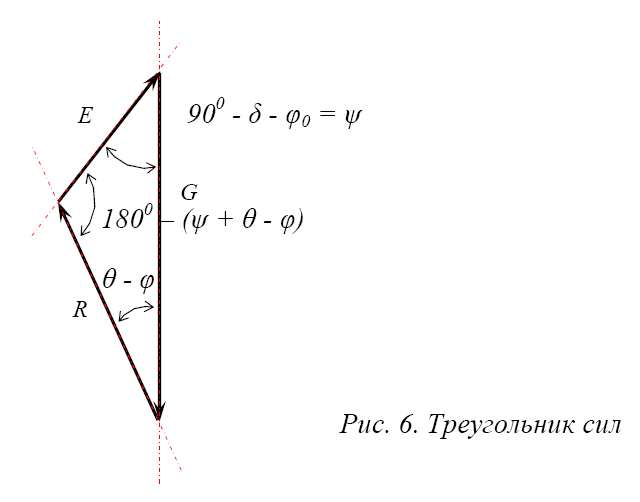
Несколько изменим на силовом треугольнике обозначения углов (рис. 6), чтобы облегчить дальнейшие преобразования.
Первоначально формула выглядела так:

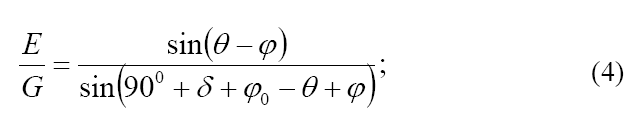
Немного по-другому преобразуем:

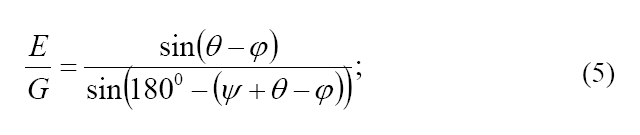
с учетом того, что sin (180⁰ – (ψ + θ – φ)) = sin(ψ + θ – φ), получим:

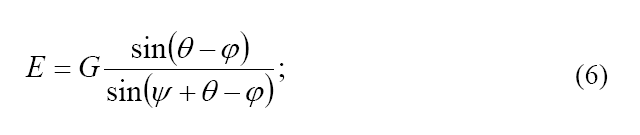
Итак, продифференцируем формулу по θ (согласно условию 3) и приравняем производную нулю.

подставим:

в результате:

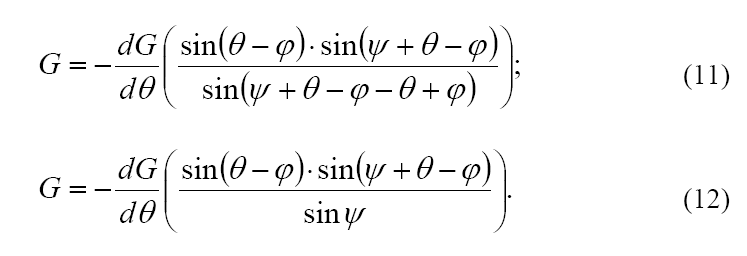
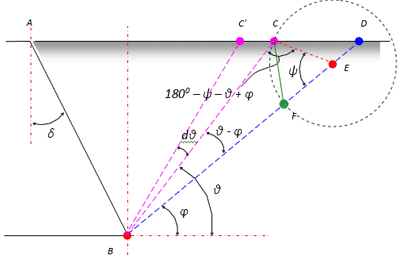
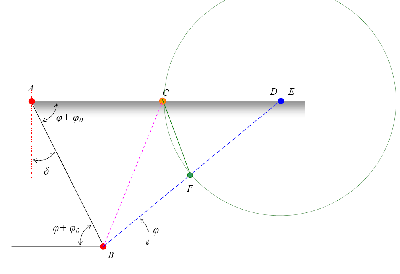
Теперь разовьем выполненное ранее (рис. 3.) построение, и обозначим на рисунке приращение dG по dθ. (рис. 7).

Рис. 7. Треугольник Ребхана

Из рисунка видно, что приращение dG = −S_{тр ВСС' ·γ} , в результате:

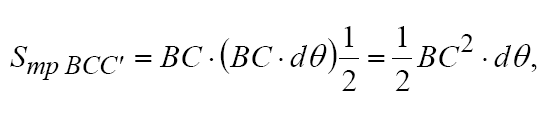
здесь S – общее обозначение площадей фигур, м².

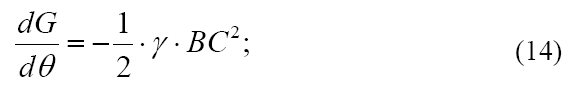
здесь γ – удельный вес грунта, кН/м³.

Знак минус показывает, что при возрастании угла θ вес G убывает.
Продолжим построение. Далее предлагается из точки С провести линию СЕ под углом ψ к линии BD. Получился треугольник ВСЕ. Из треугольника ВСЕ видно, что:

Подставим полученные зависимости (14 и 15) в основную формулу (12):

преобразуем:

при этом вспомним, что:

то есть из условия определения максимального давления, действующего на стенку, получаем:

Эта теорема известна под названием «Первая теорема Ребхана», и сформулировать её можно так:
Наиболее опасная плоскость обрушения ВС проходит таким образом, что площадь основания АВС призмы обрушения равновелика площади треугольника ВСЕ. Пользуясь этой теоремой, можно после немногих попыток найти правильное положение точки С.

Для нахождения величины давления Е продолжим построение (рис. 7).

Проведем окружность радиусом СЕ с центром в точке Е, и сделаем на линии BD засечку в точке F. Соединим точку C с точкой F. Определим площадь треугольника СЕF, приняв во внимание, что он имеет общее основание с треугольником BСЕ (площади треугольников с общей высотой относятся одна к другой как их основания):

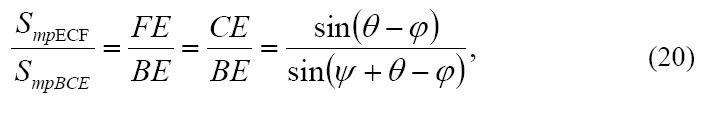
отсюда:

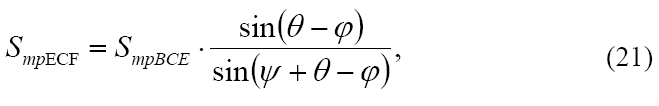
вспомним, что G = γ · S_трBCE (см. 2.17), и найдём:

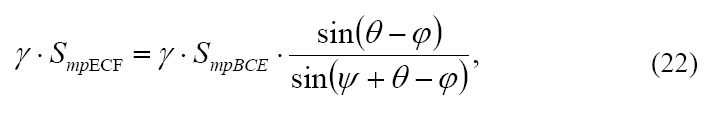
или

В этом заключается вторая изящная теорема Ребхана, которую сформулируем так:
Наибольшее давление Е равно площади треугольника ECF, умноженной на объёмный вес материала. Треугольник ECF носит название «треугольника Ребхана».

ПОСТРОЕНИЕ ПОНСЕЛЕ

Мы рассмотрели теоремы Г. Ребхана, которые помогают построить другие графические способы определения положения опасной поверхности скольжения и величины давления грунта на стенку.

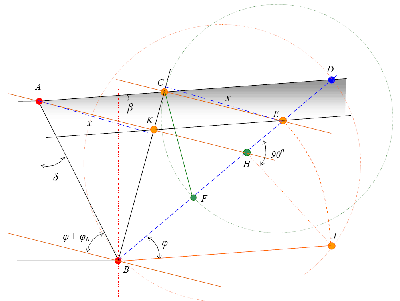
Французский ученый Ж. Понселе (рис. 1, в) предложил для случая, когда поверхность земли представляет собой плоскость, определить наибольшее давление сразу, без попыток. Для этого разовьём предложенное ранее построение.

Рис 9. Построение Понселе

1. Проводим так называемую «основную линию» под углом φ+φ₀ к задней грани стенки (рис. 9);
2. Проводим линию BD под углом внутреннего трения φ к горизонту до пересечения с поверхностью сыпучего тела;
3. На отрезке BD как на диаметре построим окружность или полуокружность;
4. Из точки А проводим прямую AH, параллельную основной линии до пересечения с линией BD в точке H;
5. Восстановить перпендикуляр в точке H к диаметру до пересечения с полуокружностью в точке J;
6. Провести окружность радиусом BJ, и в месте пересечения с линией BD сделать засечку в точке E;
7. Проводим прямую EC параллельно основной линии до пересечения с поверхностью засыпки AD. Прямая CB является изображением искомой плоскости обрушения;
8. Далее строится треугольник CEF Ребхана, который служит для определения наибольшего давления (см. вторую теорему Ребхана). Попробуем обосновать такое построение.

Хорда BJ будет среднепропорциональной между диаметром BD и прилегающим отрезком BH;
BJ² = BD·BH, при этом BJ=BE,
BE² = BD·BH; то есть (разделим на BE·BH),
BE/BH=BD/BE.
Через точку H проведём линию, параллельную основной линии и обозначим на её пересечении с прямой BC точку K.

Из подобия треугольников BCE и BKH: BC/BK = BE/BH;

*Третий признак подобия треугольников: две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а заключенные между ними углы – равны.

В результате: BD/BE = BC/BK.

Отсюда KE параллельно CD, следовательно, фигура ACEK – параллелограмм, и AK = CE.

Далее: по теореме Ребхана, площади треугольников ABC и BCE равны. У этих треугольников общее основание BC, значит, для равенства площадей необходимо, чтобы их высоты x были тоже равны. AK и EC пропорциональны этим высотам, следовательно, (при AK = EC) высоты действительно равны. Следовательно, прямая BC удовлетворяет теореме Ребхана.

Есть некоторые затруднения при решении задачи с помощью предложенного Понселе построения:

1. Случай, когда поверхность земли сама представляет собой плоскость естественного откоса (такое нередко случается в практике). То есть, когда прямые BD и AC параллельны (рис. 10).

Рис. 10. Построение Понселе для случая, когда наклон поверхности земли совпадает с наклоном плоскости естественного откоса

Точка D уходит в бесконечность, построение окружности становится невозможным. В этом случае треугольник Ребхана остается без изменения при любом наклоне плоскости скольжения BC. То есть построить треугольник FCE можно без помощи окружности с радиусом BD (точка E выбирается произвольно на линии естественного откоса – E или E’ на рис. 10). При этом сползающей призмой будет весь бесконечно большой объём грунта, заключенный между двумя параллельными плоскостями.

2. Случай, когда поверхность сыпучего тела составляет с задней гранью стены угол φ+φ⁰. Точки D и E совпадают (рис. 11).

Рис. 11. Построение Понселе для случая, когда поверхность сыпучего тела составляет с задней гранью стены угол φ+φ⁰

Однако из первой теоремы Ребхана вытекает (см. стр. 12), что в этом случае плоскость обрушения совпадает с медианой треугольника ABD(E) (площади треугольников ABC и BCE должны быть равны). То есть, для нахождения точки C достаточно разделить отрезок AD пополам.

Переведя построение Понселе «на язык анализа», можно определить давление сыпучего тела на ограждение аналитическим путем. В результате основная формула (2.24) преобразуется в вид (25).

Наиболее применяема формула, которая получается из приведенной выше для случая, когда поверхность земли – горизонтальная плоскость (β = 0), напорная грань стенки вертикальна (δ = 0), и стенка – идеально гладкая (φ⁰ = 0):

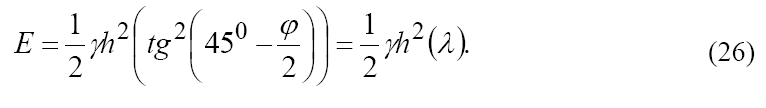
ЛИТЕРАТУРА

1. Гастев В.А. Краткий курс сопротивления материалов. – М.: Наука – 1977.
2. Глушков Г.И. Расчет сооружений, заглубленных в грунт. – М.: Стройиздат, 1977.
3. Горбачёв К.П., Краснов Е.Г., Субботницкий В.В. Основы механики деформируемого твёрдого тела. – Владивосток: Уссури, 1998.
4. Дуброва Г.А. Методы расчета давления грунтов на транспортные сооружения. – М.: Транспорт, 1969.
5. Иванов П.Л. Грунты и основания гидротехнических сооружений. Учеб. Для гидротехн. спец. вузов. – М.: ВШ, 1985.
6. Клейн Г.К. Строительная механика сыпучих тел. – М.: Стройиздат, 1977.
7. Макаров Е.В., Светлаков Н.Д. Справочные таблицы весов строительных материалов. – М.: Стройиздат, 1971.
8. Проектирование подпорных стен и стен подвалов. Справочное пособие к СниП. /ЦНИИпромзданий Госстроя СССР. – М.: Стройиздат, 1990.
9. Рабинович И.М. Основы строительной механики стержневых систем. – М.: Госстройиздат, 1960.
10. СНиП 2.06.07-87*. Подпорные стены, судоходные шлюзы, рыбопропускные и рыбозащитные сооружения. – М.: Стройиздат, 1989.
11. СНиП 2.09.03-85. Сооружения промышленных предприятий. Подземные сооружения. – М.: Стройиздат, 1985.
12. Снитко Н.К. Статическое и динамическое давление грунтов и расчет подпорных стенок. – Л.: Стройиздат, 1970.
13. Соколовский В.В. Статика сыпучей среды. – М.: Стройиздат, 1990.
14. Стоценко А.А., Доценко С.И., Мальков Н.М., Белоконь М.А. Курс Теории сооружений. Строительная механика. – Владивосток: ДВГТУ, 1994.
15. Тетиор А.Н. Подпорные стены в транспортном строительстве. – М.: Стройиздат, 1990.
16. Цытович Н.А. Механика грунтов. – М.: ВШ, 1983.