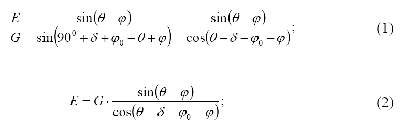Занятие 3. МЕТОДИКА РАСЧЕТА ДАВЛЕНИЯ СЫПУЧЕГО ТЕЛА НА ОГРАЖДЕНИЯ

«Задача о распределении напряжений внутри сыпучего тела и на его поверхности соприкосновения с другими телами принадлежит к числу труднейших задач строительной механики» /Рабинович И.М./ [9].

Сложность и неопределённость задачи состоят в том, что частицы, образующие упругое тело, имеют различную величину и форму, различную твердость и шероховатость; что между ними действуют силы трения, которые, в свою очередь, меняются в зависимости от степени влажности сыпучего тела. Кроме сил трения, действуют еще более неопределенные силы прилипания (сцепления).

Значительные изменения величины и направления давления земли вызывают: способ и последовательность засыпки земли позади ограждения, естественное и искусственное трамбование, случайные или систематические сотрясения грунта, малейшие осадки и перемещения стенки под влиянием собственного веса.

Становится ясно, насколько трудно в данном случае разработать приемлемые теории расчета. Поэтому все теории, предложенные до настоящего времени, оперируют с идеальным сыпучим телом (моделью), наделенным некоторыми гипотетическими однородными свойствами.

Существующие в настоящее время основные методы расчета давления сыпучего тела на ограждения основаны на предложенной в восемнадцатом веке теории Ш.О. Кулона (рис. 1, а), вошедшей в историю под кратким названием «теория Кулона». Далее рассмотрим, в чём она состоит.

1. ТЕОРИЯ КУЛОНА

Вначале перечислим упрощающие гипотезы, на которых эта теория основана:

1. Сыпучее тело (земляная масса) рассматривается как однородная сплошная среда, способная воспринимать только сжимающие и сдвигающие усилия;

Рис. 1. Учёные – инженеры, разработавшие практические методы расчёта давления сыпучего тела на ограждения

а - Кулон Шарль Огюстен (1736 - 1806): французский военный инженер. В 1781 г. сформулировал законы сухого трения;
б - Ребхан Георг (1824 - 1892): Венский профессор, инженер – строитель;
в - Понселе Жан Виктор (1788-1867): французский математик и инженер. Заложил основы проективной геометрии

2. Принимается, что при равновесии результирующее напряжение на любой площадке внутри сыпучего тела может отклоняться от нормали к площадке на угол, не превышающий некоторой величины α, которая зависит от физических свойств данного сыпучего тела. (Мы уже знаем, что этот угол равен углу внутреннего трения φ);

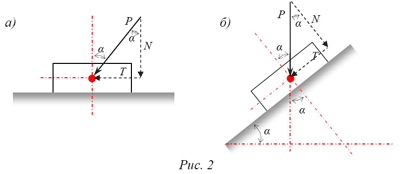
Схема к оценке состояния равновесия тела на плоскости а – горизонтальная плоскость; б – наклонная плоскость;

* Если на тело, способное скользить по плоскости, действует сила Р, наклоненная к нормали по углом α, то нормальная составляющая имеет величину N=P·cos α, сила трения из условия равновесия не может превысить величины N·f¹ = P·f ·cos α (рис. 2). Кроме того, сдвигающая сила равна T=P·;sin α. До тех пор, пока T< N·f (P·sinα < P·f ·cos α), и, или: tg α < f, тело будет только прижиматься к плоскости, но не сможет скользить. То значение угла α, при котором неравенство переходит в равенство, будет предельным для состояния равновесия (α = φ). При дальнейшем увеличении этого угла начнётся скольжение;
¹Здесь f – коэффициент трения, f = tgφ.

3. Предполагается, что стенка, уступая давлению сыпучего тела, начинает отодвигаться и определяется не то давление, которое она испытывает при обычных условиях, а то предельное, которое отвечает первому мгновению процесса отодвигания стенки. Кулон считал, что давление на стенку при обычных условиях не может превысить того, которое отвечает моменту нарушения равновесия и началу обрушения;

4. Принимается следующая гипотеза разрушения системы стенка- грунт: от сыпучего тела отделяется клин, ограниченный с одной стороны поверхностью подпорной стенки, а с другой стороны – плоскостью, проходящей через основание стенки (см. рис. 1). Эта плоскость называется плоскостью обрушения или плоскостью скольжения, а клин – призмой обрушения. Сам клин рассматривается при этом как абсолютно твёрдое тело;

5. Задача решается в условиях «плоской задачи»: предполагается, что стенка имеет неограниченную длину, и что профиль земляной массы и все прочие условия остаются по длине стенки постоянными. Таким образом, расчет ведется для участка стенки длиной 1м. Призма обрушения имеет при этом высоту, также равную единице (1м).

Наметив ограничения, мы вплотную подошли к сути теории.

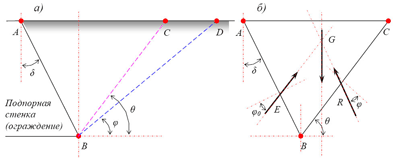
Рис. 3. Схема к определению давления сыпучего тела на ограждение а – формирование призмы (клина) обрушения; б – призма обрушения, отделённая от внешней среды

1. рассмотрим давление, оказываемое на некоторый участок АВ подпорной стенки (рис. 3);

2. проведем плоскость естественного откоса ВD;

3. вообразим, что линия ВС есть след плоскости обрушения, угол ее наклона к горизонту обозначим через θ;

4. призма обрушения «сползает» по поверхности ограждения и некоторой плоскости обрушения ВС;

5. рассмотрим момент начала сползания, когда связи между грунтом и ограждением ещё существуют, но напряжение в них – максимально. К этому случаю применяются условия равновесия, поэтому выделим призму обрушения и заменим действие отброшенных связей равнодействующими: E – в связях между ограждением и сыпучим телом; R – в связях между частицами сыпучего тела по поверхности обрушения (рис. 3, б);

6. Кроме реакций в связях, на призму обрушения действует её собственный вес (пригрузка на поверхности здесь не рассматривается): G = пл. тр. ABC · γ (здесь γ – удельный вес грунта, кН/м³);

7. В момент нарушения равновесия, когда клин начнет сползать вниз, преодолевая силы трения (силы сцепления приняты равными нулю) равнодействующие отклонятся от перпендикуляра к поверхности на соответствующий угол трения (рис. 3,б, рис. 4,а): φ – для поверхности обрушения ВС («грунт по грунту») и φ₀ – для поверхности стенки – «грунт по стенке» (угол трения грунта о стенку часто принимают равным нулю: т.е. стенка принимается идеально гладкой);

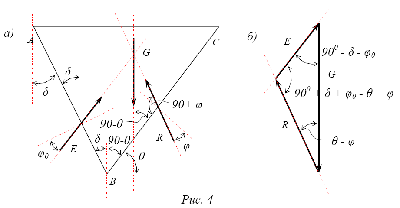
Равновесие призмы обрушения а – силы, действующие на призму обрушения; б – треугольник сил

8. Три силы – E, R и G находятся в равновесии, если они пересекаются в одной точке и треугольник сил – замкнут (рис. 4,б). Нас интересует сила E, которая противоположна давлению земли на ограждение;

9. Далее по теореме синусов:

10. Однако в правую часть выражения (2) входит неизвестный угол θ, который определяет также и вес призмы обрушения G. То есть θ является единственной независимой переменной в этой формуле. Каждому значению этого угла соответствует новое положение плоскости обрушения, новое значение веса призмы G и новое значение силы E. Необходимо определить то значение θ, при котором величина E достигает максимума. Такое значение существует, т.к. при совпадении линий ВС и ВD (когда θ = φ) призма обрушения лежит на естественном откосе и, являясь абсолютно твердым телом (см. гипотезы), не давит на стенку. В то же время при совпадении линии ВС с АВ призма обрушения не существует, следовательно G = 0 и E = 0. То есть искомая точка C лежит где-то между точками А и D.

Далее рассмотрим несколько удачных примеров дальнейшего развития теории Кулона.