Занятие 2. ПРЕДЕЛЬНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ И ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ СЫПУЧИХ ТЕЛ

Сыпучее тело, как правило, подчиняется нелинейному закону упругости и испытывает структурные деформации. Изучение поведения сыпучего тела представляет собой сложную задачу, которую обычно заменяют более простой: в которой деформации не рассматриваются совсем, а напряженное состояние принимается таким, какое бывает в начальный момент движения сыпучего тела, когда в каждой точке сыпучего тела возникает сдвиг. Такое напряженное состояние называется предельным.

Решение задачи основывается на приближенном численном решении исходных уравнений предельного равновесия:
для плоской задачи: ΣX = 0; ΣZ = 0; ΣМ = 0; после преобразований:

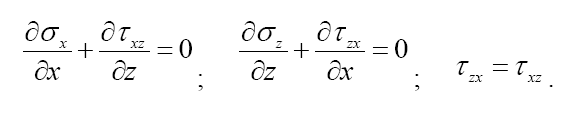
Однако, так же, как и в механике твердых тел, в механике сыпучих должен быть установлен критерий для характеристики напряженного состояния, при котором происходит разрушение или наступает текучесть. Этот критерий должен дать возможность составить дополнительные уравнения, которые в сочетании с дифференциальными уравнениями равновесия позволят определить неизвестные величины нормальных и касательных напряжений в сыпучем теле.

Этот критерий заключается в следующем: предполагается, что сыпучее тело целиком находится в предельном напряженном состоянии и в любой его точке выполняется условие предельного напряженного состояния Кулона-Мора:

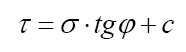
Мы видим, что условия равновесия рассматриваются в совокупности с условием, характеризующим предел прочности сыпучего тела. Построенную на этой основе теорию называют теорией предельного равновесия.

Вспомним, что через каждую точку напряженного тела можно провести три (для плоской задачи – две) взаимно перпендикулярные плоскости, по которым касательные напряжения отсутствуют, а нормальные имеют экстремальные значения. Такие плоскости называются главными площадками, а действующие по ним нормальные напряжения – главными нормальными напряжениями σ1 ;σ3

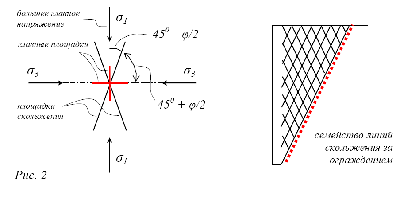
Максимальные касательные напряжения действуют под углом 45 к главным площадкам (рис. 1), и для твёрдых тел по этим площадкам может произойти сдвиг, если касательные напряжения превзойдут определенный предел. Для сыпучих же тел (где сопротивление сдвигу определяется не только величиной скрепления между частицами, но и величиной действующего сжимающего нормального напряжения), опасными в отношении сдвига будут не те площадки, по которым действуют наибольшие τ, а те, для которых отношение τ/σ (являющееся тангенсом угла θ отклонения напряжения от нормали) окажется наибольшим.

Здесь θ – угол отклонения равнодействующей полного напряжения от нормали к площадке.

Решение этой сложной задачи приведено во многих источниках [5, 6, 13] и сводится к тому, что сдвиг произойдет в том случае, если указанный угол θ достигнет величины угла внутреннего трения φ. При этом площадки скольжения будут иметь определенные углы α наклона к линиям действия главных напряжений.

Здесь α – угол наклона площадки скольжения к главной площадке.

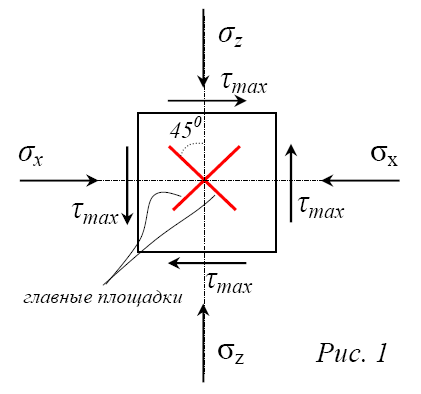
Площадки скольжения расположены симметрично по отношению к направлению действия главных напряжений и составляют с направлением действия большего главного напряжения угол 45 – φ/2 (рис. 2).

Если во всех точках сыпучего тела, образующих некоторую поверхность, наступает состояние предельного равновесия, то эта поверхность называется поверхностью скольжения. При этом весь объём, ограниченный этой поверхностью, и отделенный ею от остальной части сыпучего тела, будет находиться в состоянии предельного равновесия (решение Кулона).

Если же состояние предельного равновесия наступает во всех точках какого-либо объёма сыпучего тела, то такое состояние называется предельным напряженным состоянием (решение Соколовского). При этом в данном объеме сыпучего тела возникает бесчисленное множество поверхностей скольжения.

Иллюстрация приведенных рассуждений – графическое изображение напряжённого состояния сыпучего тела.

Круговой график напряжений (круг Мора)

В механике сыпучих сред наряду с аналитическими методами решения задач очень часто применяют графические – остроумные и замечательные.

Вычисление напряжений, действующих по наклонным площадкам в какой-либо точке, может быть заменено следующим графическим построением (рис. 3).

1. В системе прямоугольных координат σ и τ на оси σ в избранном масштабе напряжений откладываются отрезки ОА и ОВ, изображающие величины главных напряжений;

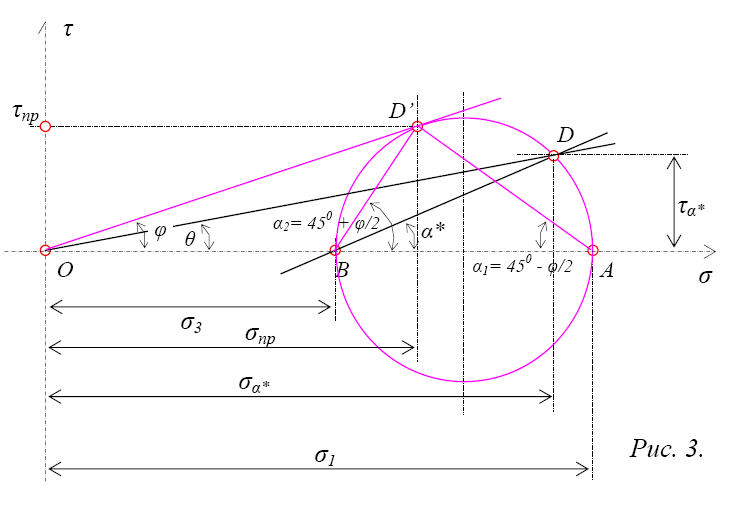
2. На отрезке АВ, равном разности σ1 и σ3, как на диаметре, строят окружность;

3. Для нахождения нормального и касательного напряжений, действующих по площадке, отклоняющейся от главной площадки на угол α*, нужно построить угол α* при точке В. Координаты точки D соответствуют нормальным и касательным напряжениям. Угол отклонения θ равнодействующей полного напряжения по площадке от нормали к ней выражается на чертеже углом, образуемым с осью σ секущей OD;

4. Для предельного равновесия сыпучего тела этот угол соответствует углу внутреннего трения φ. Из чертежа следует, что α1 = 45° - φ/2, а α2 = 45° + φ/2. Таким образом, эти углы определяют направление площадок скольжения.

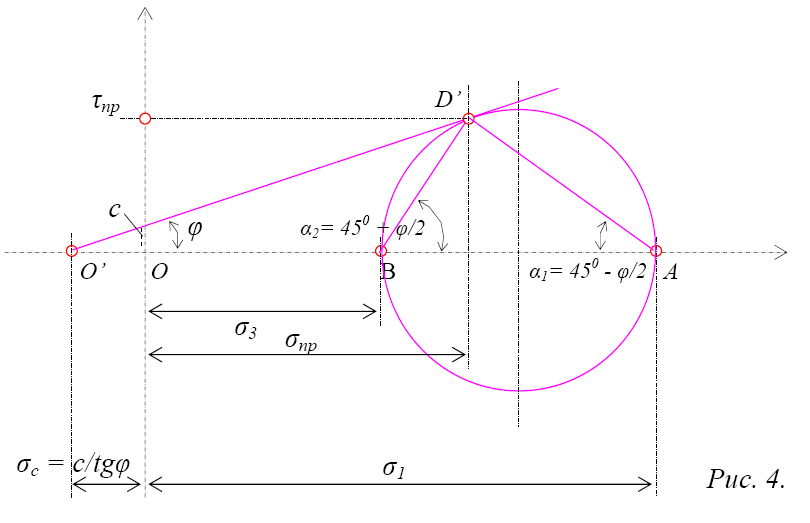
Так как предельное равновесие в какой-либо точке сыпучего тела наступает в том случае, если для двух площадок, проходящих через эту точку, будет выполняться условие α = 45° ± φ/2, то прямая OD’, проведенная под углом φ к оси σ, должна быть касательной к окружности в тех её точках, которые соответствуют данным площадкам (рис. 3).

ЛИТЕРАТУРА

1. Гастев В.А. Краткий курс сопротивления материалов. – М.: Наука – 1977.
2. Глушков Г.И. Расчет сооружений, заглубленных в грунт. – М.: Стройиздат, 1977.
3. Горбачёв К.П., Краснов Е.Г., Субботницкий В.В. Основы механики деформируемого твёрдого тела. – Владивосток: Уссури, 1998.
4. Дуброва Г.А. Методы расчета давления грунтов на транспортные сооружения. – М.: Транспорт, 1969.
5. Иванов П.Л. Грунты и основания гидротехнических сооружений. Учеб. Для гидротехн. спец. вузов. – М.: ВШ, 1985.
6. Клейн Г.К. Строительная механика сыпучих тел. – М.: Стройиздат, 1977.
7. Макаров Е.В., Светлаков Н.Д. Справочные таблицы весов строительных материалов. – М.: Стройиздат, 1971
8. Проектирование подпорных стен и стен подвалов. Справочное пособие к СниП. /ЦНИИпромзданий Госстроя СССР. – М.: Стройиздат, 1990.
9. Рабинович И.М. Основы строительной механики стержневых систем. – М.: Госстройиздат, 1960.
10. СНиП 2.06.07-87*. Подпорные стены, судоходные шлюзы, рыбопропускные и рыбозащитные сооружения. – М.: Стройиздат, 1989.
11. СНиП 2.09.03-85. Сооружения промышленных предприятий. Подземные сооружения. – М.: Стройиздат, 1985.
12. Снитко Н.К. Статическое и динамическое давление грунтов и расчет подпорных стенок. – Л.: Стройиздат, 1970.
13. Соколовский В.В. Статика сыпучей среды. – М.: Стройиздат, 1990.
14. Стоценко А.А., Доценко С.И., Мальков Н.М., Белоконь М.А. Курс Теории сооружений. Строительная механика. – Владивосток: ДВГТУ, 1994.
15. Тетиор А.Н. Подпорные стены в транспортном строительстве. – М.: Стройиздат, 1990.
16. Цытович Н.А. Механика грунтов. – М.: ВШ, 1983.