Занятие 1. РАСЧЁТНЫЕ МОДЕЛИ СПЛОШНЫХ И СЫПУЧИХ СРЕД

По своим основным физическим свойствам все тела разделяются на твёрдые, жидкие и тела, занимающие промежуточное положение между твёрдыми телами и жидкостями: это тела, которые состоят из множества отдельных более или менее однородных частиц. Такие тела называют сыпучими телами или просто сыпучими.

Сыпучие тела отличаются от твёрдых:
а) подвижностью частиц;
б) способностью сохранять форму только в известных пределах;
в) свойством оказывать давление на ограждающую поверхность;
г) неспособностью сопротивляться растяжению;
д) тем, что их способность сопротивляться сдвигающим усилиям
находится в зависимости от действия сжимающих сил.

* Жидкости отличаются от сыпучих тел большей подвижностью частиц, отсутствием постоянной формы и еще меньшей способностью сопротивляться сдвигающим усилиям.

Существуют различные модели для описания напряженного состояния указанных типов тел. К числу общих свойств, которые принимаются в моделях всех тел в большинстве дисциплин, относятся сплошность, однородность и изотропность [3].

В дальнейшем рассмотрим задачи о предельном равновесии различных сред на примере сред сыпучих, при этом рассмотрим возможность применения некоторых моделей для описания напряженного состояния сыпучих сред.

Строительная механика сыпучих сред содержит изложение способов определения давления и сопротивления сыпучей среды при различных воздействиях на него со стороны сооружения и нагрузки. В механике сыпучих сред различают два основных направления [6]:

1. Первое характеризуется введением упрощающих допущений, которые позволяют решать задачу, не прибегая к сложному математическому аппарату;
2. Второе содержит большую математическую строгость решения. Первое из указанных направлений в механике сыпучих тел содержит теории, построенные на допущении о той или иной поверхности скольжения, образующейся в толще сыпучего тела при его разрушении. Второе направление называют также теорией сыпучей среды, которая исходит из дифференциальных уравнений равновесия и условий состояния для каждой точки рассматриваемого объёма сыпучей среды [13].

Граница между этими двумя направлениями – нестабильна. Оба эти направления развиваются параллельно, существуют также промежуточные решения.

При решении задач предельного равновесия по существу рассматривается стадия разрушения сыпучего тела, поэтому в механике твёрдых деформируемых тел этой категории задач соответствуют задачи, исследуемые в теории предельного равновесия и в теории пластичности [3, 6]. При этом решение оказывается в большинстве случаев возможным без рассмотрения деформаций и перемещений сыпучего тела.

При этом в качестве основных механических характеристик среды в расчётные формулы вводят значения объёмной массы (удельный вес γ, кН/м3), внутреннего трения (угол внутреннего трения φ,0) и сцепления (удельное сцепление с, кПа). Методы определения этих характеристик рассматриваются в курсе Механики грунтов [16].

Типичной задачей этой категории будет задача об определении давления сыпучей среды на подпорные стены различных типов. Подпорная стена при этом предполагается получившей незначительное смещение, вследствие которого сыпучее тело, поддерживаемое подпорной стеной, приходит в движение (рис. 1).

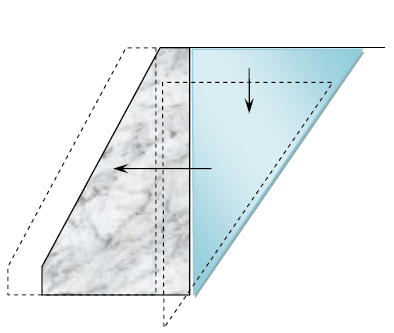
Рис. 1. Гипотеза разрушения системы «подпорная стенка – грунт»

Механика сыпучих сред во многом опирается на опыты: только из опыта могут быть получены для разных сыпучих сред числовые значения физико-механических характеристик (γ, φ, с – см. выше), входящих в расчётные формулы.

Основные расчётные модели

При разработке методов расчёта грунтовой среды (математическое описание наблюдаемых в ней процессов) приходится прибегать к схематизации рассматриваемых явлений и свойств грунтов. При этом в зависимости от поставленной задачи выделяют наиболее важные для неё факторы, а все другие не учитывают. В результате создаётся расчётная модель или расчётная схема грунта [5]. Рассмотрим основные расчётные схемы сыпучей среды:

1. Модель дискретной среды.
Вообще говоря, грунт является дискретной средой, состоящей из отдельных частиц, поэтому очень близкой к действительности оказывается модель, описывающая взаимодействие отдельных частиц с учётом связей между ними.

Пример дискретной модели: система взаимодействующих шаров или цилиндров (Г.И. Покровский, И.И. Кандауров [5]) – рис. 2. В ряде случаев эта модель применялась к крупнообломочным грунтам, например, при рассмотрении напряженного состояния каменно-набросных плотин.

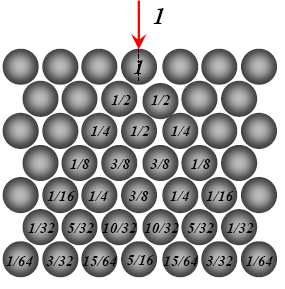
Рис. 2. Модель дискретной среды. Гипотеза долевого распределения нагрузки между отдельными элементами

2. Модель сплошной среды.
В рамках этой модели не рассматривается поведение отдельной частицы, а принимается, что составляющие грунта заполняют рассматриваемую часть пространства непрерывно. Непрерывность (континуум) строения такого идеализированного тела схраняется в процессе его деформирования.

Такая концепция сплошности вещества является основным постулатом механики сплошной среды и обеспечивает единый подход к изучению поведения твёрдых тел, сыпучих тел, жидкостей и газов. Применение модели сплошной среды к сыпучим телам позволило широко использовать имеющиеся решения теории упругости, теории пластичности и других разделов механики сплошных сред [3].

Однако, применяя к сыпучим телам концепцию сплошности, необходимо выполнять требование, чтобы принимаемые в качестве малых элементы среды имели размеры много меньше наименьших характерных размеров исследуемого пространства:

где ΔV – элементарный, бесконечно малый объём грунта, h – высота откоса (подпора), b – ширина подошвы фундамента и т.д.

В то же время для исключения влияния особенностей отдельной конкретной частицы сыпучего тела необходимо обеспечить условие:

где dmax – диаметр максимальной по крупности частицы сыпучего тела. Известно, что для большинства грунтов, являющихся основанием или внешней средой для реальных сооружений, указанные условия (1 и 2) – выполняются, что позволяет вполне обоснованно применять модель сплошной среды для описания их напряженного состояния.

ЛИТЕРАТУРА

1. Гастев В.А. Краткий курс сопротивления материалов. – М.: Наука – 1977.
2. Глушков Г.И. Расчет сооружений, заглубленных в грунт. – М.: Стройиздат, 1977.
3. Горбачёв К.П., Краснов Е.Г., Субботницкий В.В. Основы механики деформируемого твёрдого тела. – Владивосток: Уссури, 1998.
4. Дуброва Г.А. Методы расчета давления грунтов на транспортные сооружения. – М.: Транспорт, 1969.
5. Иванов П.Л. Грунты и основания гидротехнических сооружений. Учеб. Для гидротехн. спец. вузов. – М.: ВШ, 1985.
6. Клейн Г.К. Строительная механика сыпучих тел. – М.: Стройиздат, 1977.
7. Макаров Е.В., Светлаков Н.Д. Справочные таблицы весов строительных материалов. – М.: Стройиздат, 1971
8. Проектирование подпорных стен и стен подвалов. Справочное пособие к СниП. /ЦНИИпромзданий Госстроя СССР. – М.: Стройиздат, 1990.
9. Рабинович И.М. Основы строительной механики стержневых систем. – М.: Госстройиздат, 1960.
10. СНиП 2.06.07-87*. Подпорные стены, судоходные шлюзы, рыбопропускные и рыбозащитные сооружения. – М.: Стройиздат, 1989.
11. СНиП 2.09.03-85. Сооружения промышленных предприятий. Подземные сооружения. – М.: Стройиздат, 1985.
12. Снитко Н.К. Статическое и динамическое давление грунтов и расчет подпорных стенок. – Л.: Стройиздат, 1970.
13. Соколовский В.В. Статика сыпучей среды. – М.: Стройиздат, 1990.
14. Стоценко А.А., Доценко С.И., Мальков Н.М., Белоконь М.А. Курс Теории сооружений. Строительная механика. – Владивосток: ДВГТУ, 1994.
15. Тетиор А.Н. Подпорные стены в транспортном строительстве. – М.: Стройиздат, 1990.
16. Цытович Н.А. Механика грунтов. – М.: ВШ, 1983.